
| A. | (1,10)或(5,10) | B. | (-1,-2)或(3,-2) | C. | (5,10) | D. | (1,10) |
分析 计算$\overrightarrow{a}$-$\overrightarrow{b}$的坐标,根据|$\overrightarrow{a}$-$\overrightarrow{b}$|=2$\sqrt{5}$列方程解出x,利用向量不共线进行验证,再计算$\overrightarrow{c}$的坐标.
解答 解:$\overrightarrow{a}-\overrightarrow{b}$=(1-x,-4),∴|$\overrightarrow{a}-\overrightarrow{b}$|=$\sqrt{(1-x)^{2}+16}=2\sqrt{5}$,解得x=-1或x=3.
∵$\overrightarrow{a},\overrightarrow{b}$不共线,∴x≠3.即x=-1.
∴$\overrightarrow{b}$=(-1,6),
∴$\overrightarrow{c}=2\overrightarrow{a}+\overrightarrow{b}$=(2,4)+(-1,6)=(1,10).
故选:D.
点评 本题考查了平面向量的数量级运算,向量的坐标运算,属于基础题.


科目:高中数学 来源: 题型:解答题
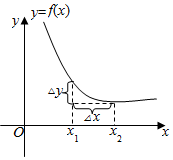 已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.
已知函数y=f(x)的图象如图,自变量x从x1变到x2,对应的函数y从f(x1)变到f(x2),设△x=x2-x1,确定各图的中△x,△y,$\frac{△y}{△x}$的正负.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在[-$\frac{π}{2}$,0]上单调递减 | B. | 函数f(x)在[0,$\frac{π}{2}$]上单调递增 | ||
| C. | 函数f(x)在[$\frac{π}{2}$,$\frac{5π}{6}$]上单调递减 | D. | 函数f(x)在[$\frac{5π}{6}$,π]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,-3),7 | B. | (-2,3),7 | C. | (2,-3),$\sqrt{7}$ | D. | (-2,3),$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
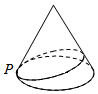 如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )
如图,一竖立在水平对面上的圆锥形物体的母线长为4m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处,则该小虫爬行的最短路程为$4\sqrt{3}m$,则圆锥底面圆的半径等于( )| A. | 1m | B. | $\frac{3}{2}m$ | C. | $\frac{4}{3}m$ | D. | 2m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com