考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求函数的导数f'(x),利用导数和函数的极值之间的关系,即可求f(x)的极大值和极小值;
(Ⅱ)当x∈(0,+∞)时,
af(x)+f′(x)<恒成立,转化求求函数的最值,即可求a的取值范围.
解答:
解:(Ⅰ)函数的定义域为R,
f'(x)=
=,
f'(x)的符号变化情况如下:
| x |
(-∞,0) |
0 |
(0,1) |
1 |
(1,4) |
4 |
(4,+∞) |
| f'(x) |
+ |
|
- |
|
+ |
|
- |
| f(x) |
递增 |
极大 |
递减 |
极小 |
递增 |
极大 |
递减 |
∴f(x)的极大值为f(0)=0和f(4)=
,
极小值为f(1)=
-.
(Ⅱ)当x∈(0,+∞)时,
af(x)+f′(x)<恒成立,
等价为a(x-2)<(x-1)(x-4)+4,
令x-2=t,则x=t+2,(t>-2),
代入上述不等式得at<a
2-t+2,
①当x>2时,x-2>0,即t>0,此时不等式等价为a
<t+-1,
∵t+
-1≥2-1=2-1,当且仅当t=
,即t=
,x=2+
时取等号.
∴a
<2-1.
②当x=2,即t=0,此时不等式at<a
2-t+2恒成立.
③当0<x<2,即-2<t<0,不等式at<a
2-t+2等价为a>t+
-1,
∵t+
-1=-[(-t)+(-
)]-1
≤-2-1=-1-2,
当且仅当-t=-
,即t=-
,即x=2-
时,等号成立.
∴a
>-1-2.
综上a的取值范围是
-1-2<a<2-1.
点评:本题主要考查函数的单调性和最值和导数之间的关系,考查学生的计算能力,运算量较大,综合性较强.



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案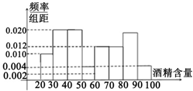 道路安全交通法规定,驾驶员血液酒精含量在20~80mg/100ml,属酒后驾车,血液酒精含量在80mg/100ml以上时,属醉酒驾车,2011年6月1日7:00至22:30,某地查处酒后驾车和醉酒驾车共50起,如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数大约为( )
道路安全交通法规定,驾驶员血液酒精含量在20~80mg/100ml,属酒后驾车,血液酒精含量在80mg/100ml以上时,属醉酒驾车,2011年6月1日7:00至22:30,某地查处酒后驾车和醉酒驾车共50起,如图是对这50人的血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数大约为( ) 如图,已知椭圆Γ:
如图,已知椭圆Γ: