
 为
为 ,射线
,射线 为
为 ,动点
,动点 在
在 的内部,
的内部, 于
于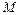 ,
, 于
于 ,四边形
,四边形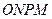 的面积恰为
的面积恰为 .
. 为定值时,动点
为定值时,动点 的纵坐标
的纵坐标 是横坐标
是横坐标 的函数,求这个函数
的函数,求这个函数 的解析式;
的解析式; 的取值范围,确定
的取值范围,确定 的定义域.
的定义域. |

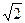 };
};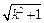
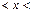
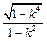 };
};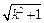
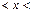
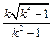 }.
}.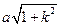 ,|ON|=
,|ON|=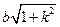 。
。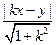 =
=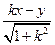 ,|PN |=
,|PN |=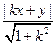 =
=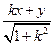
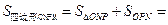
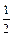 (|OM|·|PM|+|ON|·|PN|)
(|OM|·|PM|+|ON|·|PN|)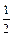 [a(kx-y)+b(kx+y)]=
[a(kx-y)+b(kx+y)]=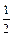 [k(a+b)x - (a-b)y]=k
[k(a+b)x - (a-b)y]=k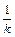 =
=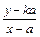 , kPN=
, kPN=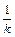 =
=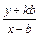 ,
, ,
,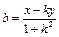 ,代入①式消a、b,并化简得x2-y2=k2+1。
,代入①式消a、b,并化简得x2-y2=k2+1。
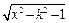 <kx
<kx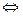
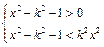
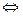
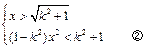 (*)
(*)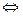 x>
x>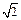 。
。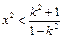 ,
,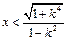 ,∴(*)
,∴(*)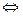
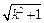
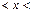
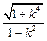 。
。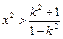 ,且
,且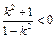 ,∴(*)
,∴(*)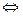
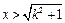
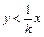 ,将它代入函数解析式,得
,将它代入函数解析式,得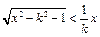
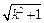
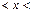
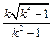 (k>1).
(k>1).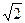 };
};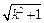
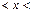
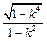 };
};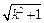
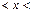
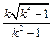 }.
}.

科目:高中数学 来源:不详 题型:解答题
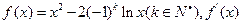 表示f(x)导函数。
表示f(x)导函数。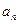 }满足
}满足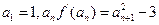 .证明:数列{
.证明:数列{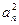 }中
}中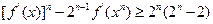 成立.
成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
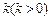 ,且知当利率为0.012时,存款量为1.44亿;又贷款的利率为
,且知当利率为0.012时,存款量为1.44亿;又贷款的利率为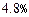 时,银行吸收的存款能全部放贷出去;若设存款的利率为
时,银行吸收的存款能全部放贷出去;若设存款的利率为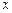 ,
,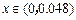 ,则当
,则当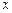 为多少时,银行可获得最大收益?
为多少时,银行可获得最大收益?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com