
已知a>0,b∈R,函数f(x)=4ax2﹣2bx﹣a+b,x∈[0,1].
(Ⅰ)当a=b=2时,求函数f(x)的最大值;
(Ⅱ)证明:函数f(x)的最大值|2a﹣b|+a;
(Ⅲ)证明:f(x)+|2a﹣b|+a≥0.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源:2016-2017学年河北定州中学高二上周练二数学试卷(解析版) 题型:解答题
如图,在四棱锥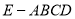 中,底面
中,底面 为正方形,
为正方形,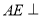 平面
平面 ,已知
,已知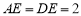 ,
, 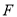 为线段
为线段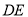 的中点.
的中点.

(1)求证: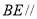 平面
平面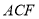 ;
;
(2)求四棱锥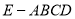 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北定州中学高二上周练二数学试卷(解析版) 题型:选择题
如图所示,正方体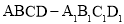 的棱长为a,M、N分别为
的棱长为a,M、N分别为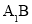 和AC上的点,
和AC上的点, ,则MN与平面
,则MN与平面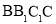 的位置关系是( )
的位置关系是( )
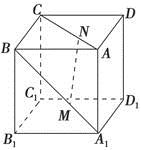
A.相交 B.平行 C.垂直 D.不能确定
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北定州中学高二上周练7.8数学试卷(解析版) 题型:解答题
如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=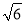 ,O为AC与BD的交点,E为棱PB上一点.
,O为AC与BD的交点,E为棱PB上一点.
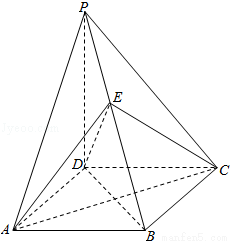
(Ⅰ)证明:平面EAC⊥平面PBD;
(Ⅱ)若PD∥平面EAC,求三棱锥P﹣EAD的体积.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北定州中学高二上周练7.8数学试卷(解析版) 题型:选择题
已知两个不重合的平面α,β和两条不同直线m,n,则下列说法正确的是( )
A.若m⊥n,n⊥α,m?β,则α⊥β
B.若α∥β,n⊥α,m⊥β,则m∥n
C.若m⊥n,n?α,m?β,则α⊥β
D.若α∥β,n?α,m∥β,则m∥n
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北定州中学高二上周练7.8数学试卷(解析版) 题型:选择题
若函数f(x)=2|x﹣a|(a∈R)满足f(1+x)=f(3﹣x),且f(x)在[m,+∞)单调递增,则实数m的最小值为( )
A.﹣2 B.﹣1 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2015-2016学年重庆八中高二暑期阶段测十数学(文)试卷(解析版) 题型:选择题
定义 ,函数
,函数 的图象与
的图象与 轴有两个不同的交点,则实数
轴有两个不同的交点,则实数 的是( )
的是( )
A. 或
或 B.
B. 或
或
C. 或
或 D.
D. 或
或
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com