[题目]函数f(x)= sin对任意x∈R.都有f+f(x+ )=0.则f( )=( )A.0B.1C.D.2 题目和参考答案——青夏教育精英家教网—

【题目】函数f（x）= sin（ωx+φ）﹣cos（ωx+φ）（0＜φ＜π，ω＞0）对任意x∈R，都有f（﹣x）+f（x）=0，f（x）+f（x+ ）=0，则f（）=（）
A.0
B.1
C.
D.2

【答案】D
【解析】解：∵f（x）= sin（ωx+φ）﹣cos（ωx+φ）=2sin（ωx+φ﹣ ），f（﹣x）+f（x）=0， ∴函数y=f（x）为奇函数，φ﹣ =kπ，k∈Z，解得：φ= +kπ，k∈Z，
∵0＜φ＜π，
∴φ= ，可得f（x）=2sinωx，
∵对任意x∈R，f（x）+f（x+ ）=0，可得：f（0）+f（）=0，
∴2sin0+2sin ω=0，解得： ω=kπ，k∈Z，解得：ω=2k，k∈Z，
∵ω＞0，不妨取k=1，可得ω=2，

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知单位圆O上的两点A，B及单位圆所在平面上的一点P，满足 =m + （m为常数）．

（1）如图，若四边形OABP为平行四边形，求m的值；
（2）若m=2，求| |的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，以坐标原点O为圆心的单位圆与x轴正半轴相交于点A，点B，P在单位圆上，且B（﹣ ，），∠AOB=α．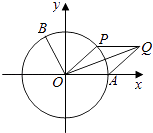

（1）求的值；
（2）设∠AOP=θ（ ≤θ≤ π）， = + ，四边形OAQP的面积为S，f（θ）=（ ﹣1）2+ S﹣1，求f（θ）的最值及此时θ的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若椭圆 + =1的焦点在x轴上，过点（1，）作圆x2+y2=1的切线，切点分别为A，B，直线AB恰好经过椭圆的右焦点和上顶点，则椭圆方程是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知A（1，）是离心率为的椭圆E： + =1（a＞b＞0）上的一点，过A作两条直线交椭圆于B、C两点，若直线AB、AC的倾斜角互补．
（1）求椭圆E的方程；
（2）试证明直线BC的斜率为定值，并求出这个定值；
（3）△ABC的面积是否存在最大值？若存在，求出这个最大值？若不存在，说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列是有关三角形ABC的几个命题，
①若tanA+tanB+tanC＞0，则△ABC是锐角三角形；
②若sin2A=sin2B，则△ABC是等腰三角形；
③若（ + ） =0，则△ABC是等腰三角形；
④若cosA=sinB，则△ABC是直角三角形；
其中正确命题的个数是（）
A..1
B..2
C.3
D.4