
【题目】已知 ![]() 的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
【答案】【解答】解:方法一(分析法):
要证 (a+b)-1+(b+c)-1=3(a+b+c)-1 ,
即证![]() ,
,
只需证![]() ,
,
化简,得![]() ,
,
即 c(b+c)+(a+b)a=(a+b)(b+c) ,
所以只需证c2+a2=b2+ac .
因为 ![]() 的三个内角A , B , C成等差数列,
的三个内角A , B , C成等差数列,
所以![]() .
.
所以![]() .
.
所以a2+c2-b2=ac .所以原式成立.
方法二(综合法):
因为 ![]() 的三个内角A , B , C成等差数列,
的三个内角A , B , C成等差数列,
所以 ![]() .
.
由余弦定理,有 b2=c2+a2-2accos600 ,
所以 c2+a2=b2+ac . .
两边加 ab+bc ,得c(b+c)+a(a+b)=(a+b)(b+c) ,
两边同时除以(a+b)(b+c) ,得 ![]() ,
,
所以![]() ,
,
即 ![]() ,
,
所以 (a+b)-1+(b+c)-1=3(a+b+c)-1 .
【解析】本题主要考查了分析法与综合法,解决问题的关键是综合法和分析法各有优缺点,从寻求解题思路来看,综合法由因导果,分析法执果索因.就表达证明过程而论,综合法形式简洁,条理清晰;分析法叙述繁琐,文辞冗长.也就是说分析法宜于思考,综合法宜于表述.因此,在实际解题时,常常把分析法和综合法结合起来运用,先利用分析法寻求解题思路,再利用综合法有条理地表述解答过程.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知长方体ABCD﹣A1B1C1D1中,底面ABCD为正方形,DD1⊥平面ABCD,AB=4,AA1=2,点E1在棱C1D1上,且D1E1=3.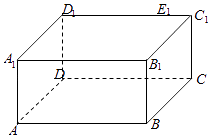
(Ⅰ)在棱CD上确定一点E,使得直线EE1∥平面D1DB,并写出证明过程;
(Ⅱ)若动点F在正方形ABCD内,且AF=2,请说明点F的轨迹,探求E1F长度的最小值并求此时直线E1F与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且an是2与Sn的等差中项.
(1)求数列{an}的通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点p(x,y)是直线kx+y+4=0(k>0)上一动点,PA、PB是圆C:x2+y2﹣2y=0的两条切线,A、B是切点,若四边形PACB的最小面积是2,则k的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com