
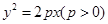 的焦点为F,直线
的焦点为F,直线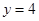 与y轴的交点为P,与C的交点为Q,且
与y轴的交点为P,与C的交点为Q,且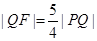 .
.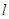 与C相交于A,B两点,若AB的垂直平分线
与C相交于A,B两点,若AB的垂直平分线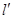 与C相较于M,N两点,且A,M,B,N四点在同一圆上,求
与C相较于M,N两点,且A,M,B,N四点在同一圆上,求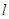 的方程.
的方程.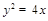 ;(2)直线
;(2)直线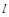 的方程为
的方程为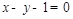 或
或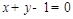 .
. 点的坐标,再由
点的坐标,再由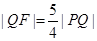 及抛物线的焦半径公式列方程可求得
及抛物线的焦半径公式列方程可求得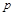 的值,从而可得抛物线C的方程;(2)由已知条件可知直线
的值,从而可得抛物线C的方程;(2)由已知条件可知直线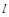 与坐标轴不垂直,故可设直线
与坐标轴不垂直,故可设直线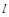 的点参式方程:
的点参式方程: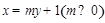 ,代入
,代入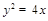 消元得
消元得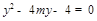 .设
.设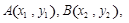 由韦达定理及弦长公式表示
由韦达定理及弦长公式表示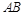 的中点
的中点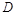 的坐标及
的坐标及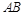 长,同理可得
长,同理可得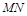 的中点
的中点 的坐标及
的坐标及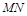 的长.由于
的长.由于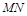 垂直平分线
垂直平分线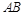 ,故
,故 四点在同一圆上等价于
四点在同一圆上等价于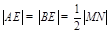 ,由此列方程可求得
,由此列方程可求得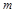 的值,进而可得直线
的值,进而可得直线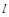 的方程.
的方程.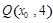 ,代入
,代入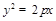 ,得
,得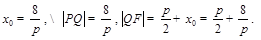 .由题设得
.由题设得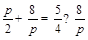 ,解得
,解得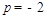 (舍去)或
(舍去)或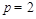 ,∴C的方程为
,∴C的方程为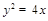 ;(2)由题设知
;(2)由题设知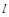 与坐标轴不垂直,故可设
与坐标轴不垂直,故可设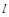 的方程为
的方程为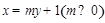 ,代入
,代入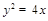 得
得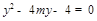 .设
.设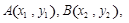 则
则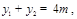
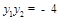 .故
.故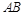 的中点为
的中点为 .又
.又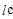 的斜率为
的斜率为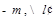 的方程为
的方程为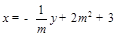 .将上式代入
.将上式代入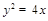 ,并整理得
,并整理得 .设
.设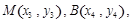 则
则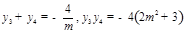 .故
.故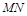 的中点为
的中点为 .
.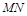 垂直平分线
垂直平分线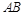 ,故
,故 四点在同一圆上等价于
四点在同一圆上等价于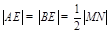 ,从而
,从而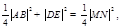 即
即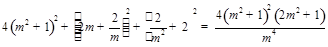 ,化简得
,化简得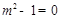 ,解得
,解得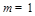 或
或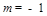 .所求直线
.所求直线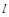 的方程为
的方程为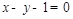 或
或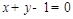 .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源:不详 题型:解答题
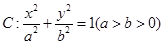 经过点
经过点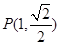 ,且两焦点与短轴的两个端点的连线构成一正方形.(12分)
,且两焦点与短轴的两个端点的连线构成一正方形.(12分)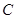 的方程;
的方程;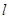 与椭圆
与椭圆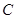 交于
交于 ,
,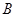 两点,若线段
两点,若线段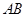 的垂直平分线经过点
的垂直平分线经过点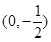 ,求
,求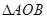
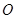 为原点)面积的最大值.
为原点)面积的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
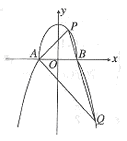
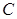 由上半椭圆
由上半椭圆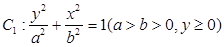 和部分抛物线
和部分抛物线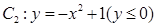 连接而成,
连接而成,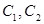 的公共点为
的公共点为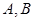 ,其中
,其中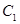 的离心率为
的离心率为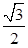 .
.
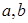 的值;
的值;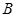 的直线
的直线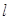 与
与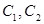 分别交于
分别交于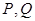 (均异于点
(均异于点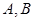 ),若
),若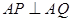 ,求直线
,求直线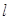 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
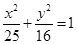 的右焦点为
的右焦点为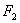 ,点
,点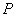 是椭圆上任意一点,圆
是椭圆上任意一点,圆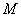 是以
是以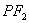 为直径的圆.
为直径的圆.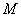 过原点
过原点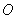 ,求圆
,求圆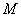 的方程;
的方程; 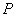 在椭圆的什么位置,该定圆总与圆
在椭圆的什么位置,该定圆总与圆 相切,请写出你的探究过程.
相切,请写出你的探究过程. 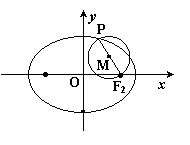
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
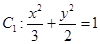 的左右焦点为
的左右焦点为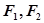 ,直线
,直线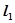 过点
过点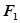 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线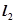 垂直于直线
垂直于直线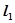 于点P,线段
于点P,线段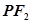 的垂直平分线与
的垂直平分线与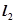 的交点的轨迹为曲线
的交点的轨迹为曲线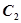 ,若
,若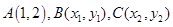 是
是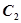 上不同的点,且
上不同的点,且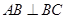 ,则
,则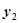 的取值范围是( )
的取值范围是( )A.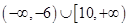 | B.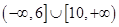 |
C.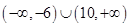 | D.以上都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com