
【题目】已知函数![]() 的图像关于直线
的图像关于直线![]() 对称,且
对称,且![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)若将![]() 图像上各点的横坐标变为原来的
图像上各点的横坐标变为原来的![]() ,再将所得图像向右平移
,再将所得图像向右平移![]() 个单位,得到
个单位,得到![]() 的图像,且关于
的图像,且关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]()
(2)![]() 或
或![]()
【解析】
(1)由三角恒等变换可得![]()
![]() ,再结合函数
,再结合函数![]() 图像的对称性即可求出
图像的对称性即可求出![]() ;
;
(2)由三角函数图像的变换可得:将![]() 图像上各点的横坐标变为原来的
图像上各点的横坐标变为原来的![]() ,再将所得图像向右平移
,再将所得图像向右平移![]() 个单位,得到
个单位,得到![]() 的图像,则
的图像,则![]() ,再作出函数
,再作出函数![]() 在区间
在区间![]() 的图像,再观察函数
的图像,再观察函数![]() 的图像与直线
的图像与直线![]() 在区间
在区间![]() 上的交点个数即可.
上的交点个数即可.
解:(1)因为![]()
![]() ,
,
又函数![]() 的图像关于直线
的图像关于直线![]() 对称,
对称,
则![]() ,解得
,解得![]() ,
,
又![]() ,即
,即![]() ,
,
即![]()
![]() ,
,
(2)将![]() 图像上各点的横坐标变为原来的
图像上各点的横坐标变为原来的![]() ,得函数图像所对应的解析式为
,得函数图像所对应的解析式为![]()
![]() ,再将所得图像向右平移
,再将所得图像向右平移![]() 个单位,得到
个单位,得到![]() 的图像,则
的图像,则![]() ,
,
由关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有且只有一个实数解,
上有且只有一个实数解,
则函数![]() 的图像与直线
的图像与直线![]() 在区间
在区间![]() 上有且只有一个交点,
上有且只有一个交点,
又函数![]() 在区间
在区间![]() 上的图像如图所示,
上的图像如图所示,
则数![]() 的图像与直线
的图像与直线![]() 在区间
在区间![]() 上有且只有一个交点时,
上有且只有一个交点时,![]() 或
或![]() ,
,
即实数![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
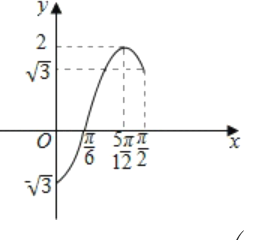


科目:高中数学 来源: 题型:
【题目】设F1,F2分别是椭圆E: ![]() (a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=
(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=![]() ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为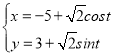 ,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线l的极坐标方程为
,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线l的极坐标方程为![]() ,A,B两点的极坐标分别为
,A,B两点的极坐标分别为![]() .
.
(1)求圆C的普通方程和直线l的直角坐标方程;
(2)点P是圆C上任一点,求△PAB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() .
.
(Ⅰ)求函数![]() 在R上的解析式;
在R上的解析式;
(Ⅱ)若![]() ,函数
,函数![]() ,是否存在实数m使得
,是否存在实数m使得![]() 的最小值为
的最小值为![]() ,若存在,求m的值;若不存在,请说明理由.
,若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
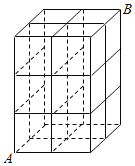
【题目】如图,某建筑工地搭建的脚手架局部类似于一个![]() 的长方体框架,一个建筑工人欲从
的长方体框架,一个建筑工人欲从![]() 处沿脚手架攀登至
处沿脚手架攀登至 ![]() 处,则其最近的行走路线中不连续向上攀登的概率为( )
处,则其最近的行走路线中不连续向上攀登的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
A. 6种 B. 24种 C. 30种 D. 36种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com