
| A. | $\frac{ln5-ln3}{8}$ | B. | $\frac{ln3}{4}$ | C. | $\frac{ln5+ln3}{8}$ | D. | $\frac{ln4}{3}$ |
分析 由f(m)=f(n)⇒2lnn-an2+3=2lnm-am2+3,得a=$\frac{lnn-lnm}{{n}^{2}-{m}^{2}}$.令n=m+t,(t≥1),则a=$\frac{ln(1+\frac{t}{m})}{t(2m+t)}$,显然g(m)═$\frac{ln(1+\frac{t}{m})}{t(2m+t)}$,在m∈[1,+∞)单调递减,得a≤g(1)=$\frac{ln(1+t)}{t(2+t)}$,(t≥2)
令h(t)=g(1)=$\frac{ln(1+t)}{t(2+t)}$,(t≥2),h′(t)=$\frac{{t}^{2}+2t-2ln(t+1)(t+1)^{2}}{[t(t+2)]^{2}(t+1)}$,根据h(t)的单调性求得实数a的最大值.
解答 解:由f(m)=f(n)⇒2lnn-an2+3=2lnm-am2+3,∴a=$\frac{lnn-lnm}{{n}^{2}-{m}^{2}}$.
令n=m+t,(t≥1),则a=$\frac{ln(1+\frac{t}{m})}{t(2m+t)}$,(m∈[1,5],t≥2)
显然g(m)═$\frac{ln(1+\frac{t}{m})}{t(2m+t)}$,在m∈[1,+∞)单调递减,∴a≤g(1)=$\frac{ln(1+t)}{t(2+t)}$,(t≥1)
令h(t)=g(1)=$\frac{ln(1+t)}{t(2+t)}$,(t≥2),h′(t)=$\frac{{t}^{2}+2t-2ln(t+1)(t+1)^{2}}{[t(t+2)]^{2}(t+1)}$
∵t≥2,∴2ln(t+1)>1,则t2+2t-2ln(t+1)(t+1)2<0,
∴令h(t)=g(1)=$\frac{ln(1+t)}{t(2+t)}$,(t≥2),单调递减,
∴$a≤h(2)=\frac{ln3}{4}$
∴实数a的最大值为$\frac{ln3}{4}$.
故选:B
点评 本题考查了利用导数求函数的单调性、最值,考查了转化思想,计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 购买商品金额 | 折扣 |
| 消费不超过200元的部分 | 9折 |
| 消费超过200元但不超过500元的部分 | 8折 |
| 消费超过500元但不超过1000元的部分 | 7折 |
| 消费超过1000元的部分 | 6折 |
| 购买商品金额 | (0,200] | (200,500] | (500,1000] | 1000以上 |
| 人数 | 10 | 40 | 30 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
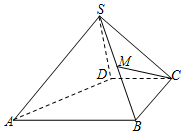 如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.
如图,四棱锥S-ABCD中,M是SB的中点,AB∥CD,BC⊥CD,SD⊥面SAB,且AB=BC=2CD=2SD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{10}$-$\frac{11}{10}$i | B. | -$\frac{3}{10}$+$\frac{11}{10}$i | C. | $\frac{3}{10}$+$\frac{11}{10}$i | D. | $\frac{3}{10}$-$\frac{11}{10}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com