练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如下图,四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=2,EF⊥AB,则EF与CD所成的角等于___________.

    答案:30°

    解析:取AD的中点G，连结EG、FG，易知EG=1，FG=.

    由EF⊥AB及GF∥AB知EF⊥FG.

    在Rt△EFG中，求得∠GEF=30°，即为EF与CD所成的角.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高三数学教学与测试 题型：044

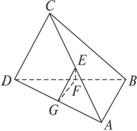
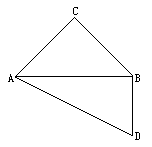
    将一副三角板放在同一个平面上组成下图所示的四边形ACBD，△ABC中，∠C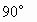＝，AC＝BC，△ABD中，∠AB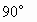D＝，∠D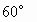＝．设AC＝a．现将四边形ACBD沿着AB翻折成直二面角C－AB－D，连结CD得一个四面体(如下图)．

    　　

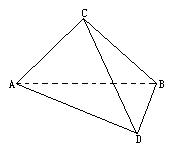
    (1)求证：平面ACD⊥平面BCD；

    (2)求直线AD和BC所成的角；

    (3)求直线AD和平面BCD所成的角；

    (4)求平面ACD和平面ABD所成二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源：广东省梅县东山中学2011－2012学年高二上学期期中考试数学理科试题 题型：013

    如下图，AB是⊙O的直径，C是圆周上不同于A、B的任意一点，PA⊥平面ABC，则四面体P－ABC的四个面中，直角三角形的个数有

    [　　]
    A．

    4个

    B．

    3个

    C．

    2个

    D．

    1个

    查看答案和解析>>

    科目：高中数学 来源：英德中学2005～2006年高二数学选修(2－1)期末模拟考试题 题型：044

    如下图所示，在四面体P－ABC中，已知PA＝BC＝6，PC＝AB＝10，AC＝8，PB＝．F是线段PB上一点，，点E在线段AB上，且EF⊥PB．

    (Ⅰ)证明：PB⊥平面CEF；

    (Ⅱ)求二面角B－CE－F的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

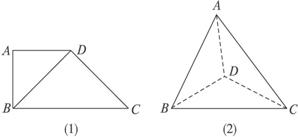
    如下图(1),四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,如下图(2),则在四面体ABCD中,下列命题正确的是(    )

    A.平面ABD⊥平面ABC                        B.平面ADC⊥平面BDC

    C.平面ABC⊥平面BDC                        D.平面ADC⊥平面ABC

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，在四面体O—ABC中,=a,=b,=c,D为BC中点,E为AD的中点,则=_____.(用a,b,c表示)

    查看答案和解析>>

    同步练习册答案