
分析 根据题意,(1)若三个偶数必相邻,分3步进行分析:①、先将1、3、5、7四个奇数数字全排列,排好后,有5个空位可选,②、将3个偶数数字看成一个整体,③、在5个空位中任选1个,安排3个偶数数字这个整体,由分步计数原理计算可得答案,
若三个偶数互不相邻,分2步进行分析:①、先将1、3、5、7四个奇数数字全排列,有5个空位可选,②、在5个空位中,任选3个,安排三个偶数数字,由分步计数原理计算可得答案,
(2)①、由平均分组公司直接计算即可得答案;
②、分3步分析:先在6本书中先取出1本,作为一组,再在剩下的5本书中取出2本,作为一组,最后将余下的3本作为1组,由分步计数原理计算可得答案.
解答 解:(1)根据题意,若三个偶数必相邻,分3步进行分析:
①、先将1、3、5、7四个奇数数字全排列,有A44=24种情况,
排好后,有5个空位可选,
②、将3个偶数数字看成一个整体,考虑其顺序,有A33=6种情况,
③、在5个空位中任选1个,安排3个偶数数字这个整体,有5种情况,
则三个偶数必相邻的七位数有24×6×5=720个;
若三个偶数互不相邻,分2步进行分析:
①、先将1、3、5、7四个奇数数字全排列,有A44=24种情况,
排好后,有5个空位可选,
②、在5个空位中,任选3个,安排三个偶数数字,有A53=60种情况,
则三个偶数互不相邻的七位数有24×60=1440种;
(2)①根据题意,将6本书分成3组,每组2本,即将6本书平均分成3组,
有$\frac{C_6^2C_4^2C_2^2}{A_3^3}$=15种分组方法;
②将6本书分成3组,一组一本,一组二本,一组三本,
在6本书中先取出1本,作为一组,有C61种分发,
在剩下的5本书中取出2本,作为一组,有C52种分发,
将最后的3本作为1组,有C33种情况,
则共有$C_6^1C_5^2C_3^3$=60种分法.
点评 本题考查排列、组合的实际应用,(2)中注意平均分组与不平均分组公司的不同.


科目:高中数学 来源: 题型:选择题
| A. | {x|x<3} | B. | {x|x≥5} | C. | {x|3≤x≤5} | D. | {x|3<x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{9}{8}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
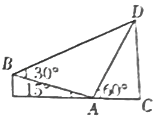 如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.
如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,4} | B. | {3,6} | C. | {1,3} | D. | {1,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com