
·ÖÎö Éè$\overrightarrow{c}$=£¨x£¬y£©£¬¸ù¾ƯỊ̈Á¿ÊưÁ¿»ưµÄ´¹Ö±µÄµÈ¼Û̀ơ¼₫£¬Çó³öx£¬yÂú×ăµÄ̀ơ¼₫£¬½áºÏ|$\overrightarrow{c}$|µÄ¼¸ºÎ̉ẩå½øĐĐÇó½â¼´¿É£®
½â´đ 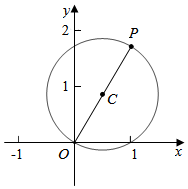 ½â£ºÉè$\overrightarrow{c}$=£¨x£¬y£©£¬Ộ$\overrightarrow{a}$-$\overrightarrow{c}$=£¨1-x£¬-y£©£¬$\overrightarrow{b}$-$\overrightarrow{c}$=£¨-x£¬$\sqrt{3}$-y£©£¬
½â£ºÉè$\overrightarrow{c}$=£¨x£¬y£©£¬Ộ$\overrightarrow{a}$-$\overrightarrow{c}$=£¨1-x£¬-y£©£¬$\overrightarrow{b}$-$\overrightarrow{c}$=£¨-x£¬$\sqrt{3}$-y£©£¬
¡ß£¨$\overrightarrow{a}$-$\overrightarrow{c}$£©•£¨$\overrightarrow{b}$-$\overrightarrow{c}$£©=0£¬
¡à£¨1-x£¬-y£©•£¨-x£¬$\sqrt{3}$-y£©=0£¬
¼´-x£¨1-x£©-y£¨$\sqrt{3}$-y£©=0
¼´x2-x+y2-$\sqrt{3}$y=0£¬
¼´£¨x-$\frac{1}{2}$£©2+£¨y-$\frac{\sqrt{3}}{2}$£©2=1£¬
ỘÔ²ĐÄC£¨$\frac{1}{2}$£¬$\frac{\sqrt{3}}{2}$£©£¬
Ộ|$\overrightarrow{c}$|=$\sqrt{{x}^{2}+{y}^{2}}$£¬Ộ|$\overrightarrow{c}$|µÄ¼¸ºÎ̉ẩåÊÇÔ²CÉÏµÄµăµ½ÔµăµÄ¾àÀ룬
Ộ|OC|=$\sqrt{£¨\frac{1}{2}£©^{2}+£¨\frac{\sqrt{3}}{2}£©^{2}}$=1£¬
Ộ|$\overrightarrow{c}$|µÄ×î´óÖµÊÇ|OC|+1=1+1=2£¬
¹Ê´đ°¸Îª£º2
µăÆÀ ±¾̀âÖ÷̉ª¿¼²éÊưÁ¿»ưµÄÓ¦ÓĂ£¬¸ù¾ƯỊ̈Á¿´¹Ö±µÄµÈ¼Û̀ơ¼₫£¬ÀûÓĂÊưĐνáºÏÊǽâ¾ö±¾̀âµÄ¹Ø¼ü£®



| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
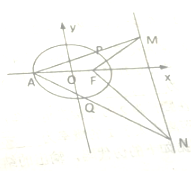 Èçͼ£¬̉ÑÖªÍÖÔ²C£º$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1£¨a£¾b£¾0£©¹ưµă£¨1£¬$\frac{3}{2}$£©£¬Ç̉ÀëĐÄÂÊe=$\frac{1}{2}$£¬¹ưÍÖÔ²Ó̉½¹µăF×÷»¥Ïà´¹Ö±µÄÁ½Ö±ÏßÓëÆäÓ̉×¼Ïß½»ÓÚµăM¡¢N£¬AΪÍÖÔ²µÄ×ó¶¥µă£¬Á¬½ÓAM¡¢AN½»ÍÖÔ²ÓÚP£¬QÁ½µă£®
Èçͼ£¬̉ÑÖªÍÖÔ²C£º$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1£¨a£¾b£¾0£©¹ưµă£¨1£¬$\frac{3}{2}$£©£¬Ç̉ÀëĐÄÂÊe=$\frac{1}{2}$£¬¹ưÍÖÔ²Ó̉½¹µăF×÷»¥Ïà´¹Ö±µÄÁ½Ö±ÏßÓëÆäÓ̉×¼Ïß½»ÓÚµăM¡¢N£¬AΪÍÖÔ²µÄ×ó¶¥µă£¬Á¬½ÓAM¡¢AN½»ÍÖÔ²ÓÚP£¬QÁ½µă£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | W¡Ü1 | B£® | W£¼1 | C£® | W¡Ư1 | D£® | W£¾1 |
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com