
分析 (I)利用倍角公式与和差公式可得f(x)=$2sin(2x+\frac{π}{6})$+1,再利用三角函数的周期性、单调性即可得出.
(II)由(I)可知$f({x_0})=2sin(2{x_0}+\frac{π}{6})+1=\frac{11}{5}$,可得$sin(2{x}_{0}+\frac{π}{6})$=$\frac{3}{5}$,由x0∈[${\frac{π}{4}$,$\frac{π}{2}}$],可得$2{x}_{0}+\frac{π}{6}$∈$[\frac{2π}{3},\frac{7π}{6}]$.可得$cos(2{x_0}+\frac{π}{6})=-\frac{4}{5}$.再利用弧长公式即可得出.
解答 解:(I)由$f(x)=\sqrt{3}sin2x+2{cos^2}x(x∈R)$,得$f(x)=2×\frac{1}{2}\sqrt{3}sin2x+2{cos^2}x+1-1=2sin(2x+\frac{π}{6})+1$,
∴函数f(x)的最小正周期为π.
由$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$得单调增区间是:$[{-\frac{π}{3}+kπ,\frac{π}{6}+kπ}]$,k∈z.
(Ⅱ)由(1)可知$f({x_0})=2sin(2{x_0}+\frac{π}{6})+1=\frac{11}{5}$
得$sin(2{x}_{0}+\frac{π}{6})$=$\frac{3}{5}$,
∵x0∈[${\frac{π}{4}$,$\frac{π}{2}}$],∴$2{x}_{0}+\frac{π}{6}$∈$[\frac{2π}{3},\frac{7π}{6}]$.
∴$cos(2{x_0}+\frac{π}{6})=-\frac{4}{5}$.
∴sin(2x0-$\frac{π}{12}$)=$sin[{(2{x_0}+\frac{π}{6})-\frac{π}{4}}]$
=$sin(2{x}_{0}+\frac{π}{6})cos\frac{π}{4}$-$cos(2{x}_{0}+\frac{π}{6})$$sin\frac{π}{4}$
=$\frac{7\sqrt{2}}{10}$.
点评 本题考查了三角函数的图象与性质、倍角公式、和差公式、三角函数求值,考查了推理能力与计算能力,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 2或3 | D. | 4或9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-2,2) | C. | (-1,5) | D. | (-2,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
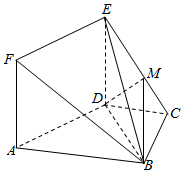 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,点M在线段EC上.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,点M在线段EC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE,分别交⊙O于D、G两点,连接DG交CB于点F.
如图,AB是⊙O的直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE,分别交⊙O于D、G两点,连接DG交CB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
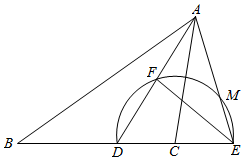 已知在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
已知在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com