
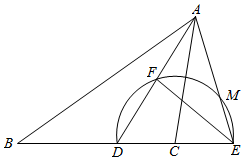
 已知在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.
已知在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3.分析 (Ⅰ)欲证AF=DF,可以证明△AEF≌△DEF得出;
(Ⅱ)求∠AED的余弦值,即求ME:DM,由已知条件,勾股定理,切割线定理的推论可以求出.
解答  证明:(Ⅰ)∵AD平分∠BAC,
证明:(Ⅰ)∵AD平分∠BAC,
∴∠BAD=∠DAC.
∵∠B=∠CAE,
∴∠BAD+∠B=∠DAC+∠CAE
∵∠ADE=∠BAD+∠B,
∴∠ADE=∠DAE.
∴EA=ED.
∵DE是半圆C的直径,
∴∠DFE=90°.
∴AF=DF.…(5分)
解:(Ⅱ)连结DM,
∵DE是半圆C的直径,
∴∠DME=90°.
∵FE:FD=4:3,
∴可设FE=4x,则FD=3x.
由勾股定理,得DE=5x.
∴AE=DE=5x,AF=FD=3x
∵AF•AD=AM•AE
∴3x(3x+3x)=AM•5x
∴AM=3.6x
∴ME=AE-AM=5x-3.6x=1.4x
在Rt△DME中,cos∠AED=$\frac{ME}{DE}$=$\frac{7}{25}$.…(10分)
点评 本题考查相似三角形的判定,切割线定理,勾股定理,圆周角定理等知识点的综合运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
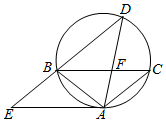 如图,△ABC为圆内接三角形,BD为圆的弦,且BD∥AC,过点A做圆的切线与DB的延长线交于点E,AD与BC交于点F,若AB=AC=4,BD=5,则$\frac{AF}{FD}$=$\frac{4}{5}$;AE=6.
如图,△ABC为圆内接三角形,BD为圆的弦,且BD∥AC,过点A做圆的切线与DB的延长线交于点E,AD与BC交于点F,若AB=AC=4,BD=5,则$\frac{AF}{FD}$=$\frac{4}{5}$;AE=6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
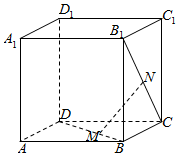 如图,正方体ABCD-A1B1C1D1的所有棱长都为1,M、N分别为线段BD和B1C上的两个动点.
如图,正方体ABCD-A1B1C1D1的所有棱长都为1,M、N分别为线段BD和B1C上的两个动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
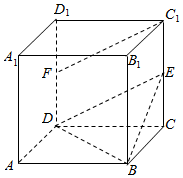 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F分别是棱CC1与DD1的中点
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F分别是棱CC1与DD1的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
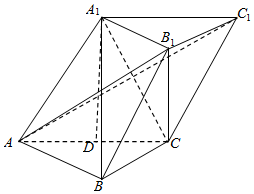 如图,三棱柱中ABC-A1B1C1中,点A1在平面ABC内的射影D是棱AC的中点,侧面AA1C1C为边长为2的菱形,且BC=1,∠ACB=90°.
如图,三棱柱中ABC-A1B1C1中,点A1在平面ABC内的射影D是棱AC的中点,侧面AA1C1C为边长为2的菱形,且BC=1,∠ACB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com