
 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望; .
. 的概率分布为
的概率分布为 | 2 | 3 | 4 | 5 |
 |  | 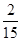 |  |  |
 的数学期望为
的数学期望为
 。
。 ,则事件
,则事件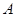 和事件
和事件 是互斥事件,因为
是互斥事件,因为 ,所以
,所以 .
. 有可能的取值为:2,3,4,5.
有可能的取值为:2,3,4,5.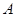 ,
,
 ,则事件
,则事件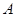 和事件
和事件 是互斥事件,因为
是互斥事件,因为 ,所以
,所以 .
. 有可能的取值为:2,3,4,5.
有可能的取值为:2,3,4,5.



 的概率分布为
的概率分布为 | 2 | 3 | 4 | 5 |
 |  | 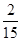 |  |  |
 的数学期望为
的数学期望为
 ,则
,则


科目:高中数学 来源:不详 题型:解答题
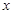 个红球与
个红球与 个白球(
个白球( ,且
,且 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。 ,求当
,求当 取得最大值时的
取得最大值时的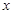 ,
, 的值;
的值; 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数 的期望
的期望 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 . 当
. 当 为何值时, 其发生的概率最大? 说明理由;
为何值时, 其发生的概率最大? 说明理由;  . 求
. 求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.  :集合中的所有元素之和为10,求所取出的非空子集满足性质
:集合中的所有元素之和为10,求所取出的非空子集满足性质 的概率;
的概率; ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 、
、 、
、 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为 ,对乙项目投资十万元,
,对乙项目投资十万元,  取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量 、
、 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润. 、
、 的概率分布和数学期望
的概率分布和数学期望 、
、 ;
; 时,求
时,求 的取值范围.
的取值范围. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列与数学期望.
的分布列与数学期望. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 表示4名乘客在第4层下电梯的人数,则
表示4名乘客在第4层下电梯的人数,则 的数学期望为 ,方差为 .
的数学期望为 ,方差为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 。
。 的分布列与数学期望。
的分布列与数学期望。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com