
 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 。
。 的分布列与数学期望。
的分布列与数学期望。 | 0 | 1 | 2 |
| P | 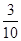 | 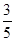 | 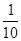 |
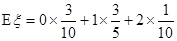 =
=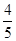 .
. 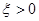 为不可能事件,显然不符合题意-------------------------------(4分)
为不可能事件,显然不符合题意-------------------------------(4分)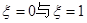 是对立事件,且
是对立事件,且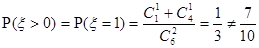
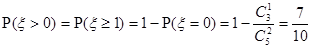 符合题意。----(8分)
符合题意。----(8分) 的可能取值为0,1,2 -----------------------------------------------------(10分)
的可能取值为0,1,2 -----------------------------------------------------(10分)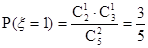 ,------------------------------------------------(11分)
,------------------------------------------------(11分) ,--------------------------------------------------(12分)
,--------------------------------------------------(12分) | 0 | 1 | 2 |
| P | 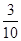 | 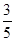 | 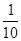 |
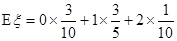 =
=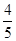 . -------------------------------(14分)
. -------------------------------(14分)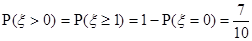 ,∴
,∴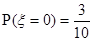 .……………(3分)
.……………(3分)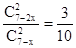 .∴
.∴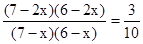 .∴x=2.
.∴x=2. 的可能取值为0,1,2 -----------------------------------------------------(6分)
的可能取值为0,1,2 -----------------------------------------------------(6分)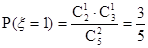 ,---------------------------------------------------(7分)
,---------------------------------------------------(7分) ,----------------------------------------------------(8分)
,----------------------------------------------------(8分) | 0 | 1 | 2 |
| P | 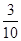 | 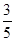 | 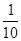 |
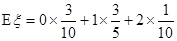 =
=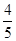 . -------------------------------(10分)
. -------------------------------(10分) 

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 4 | 4 | 3 | 1 |
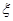 ,求随机变量
,求随机变量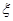 的分布列和数学期望
的分布列和数学期望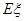 .(8分)
.(8分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
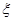 .
.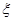 的分布列;
的分布列;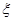 的数学期望);
的数学期望); ,一等品率提高为
,一等品率提高为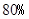 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 参加次数 | 0 | 1 | 2 | 3 |
| 人数 | 0.1 | 0.2 | 0.4 | 0.3 |
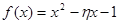 在区间
在区间 ,
, 内有零点”的事件为
内有零点”的事件为 ,求
,求 发生的概率
发生的概率 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com