
 ,求
,求 的分布列与数学期望.
的分布列与数学期望. 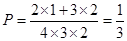 ;
; 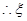 的分布列为
的分布列为 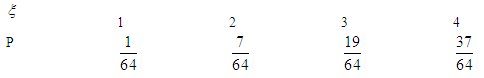
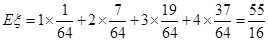
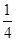 )3+C 23 (
)3+C 23 (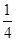 )2(k-
)2(k-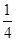 )+3 (
)+3 (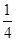 )(k-
)(k- 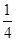 )2求出相应的概率,列出分布列,最后利用数学期望公式进行求解即可
)2求出相应的概率,列出分布列,最后利用数学期望公式进行求解即可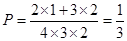
 的可能取值为1,2,3,4
的可能取值为1,2,3,4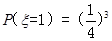
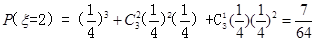
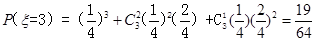
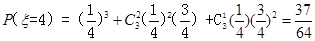
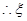 的分布列为
的分布列为 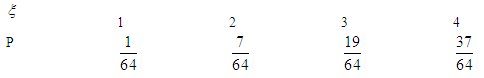


科目:高中数学 来源:不详 题型:解答题
| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.05 |
| [25,30) | ① | 0.20 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.30 |
| [40,45] | 10 | 0.10 |
| 合计 | 100 | 1.00 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用). 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
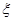 .
.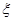 的分布列;
的分布列;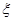 的数学期望);
的数学期望); ,一等品率提高为
,一等品率提高为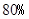 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com