
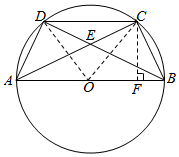
 如图,D、C是以AB为直径的⊙O上被AB分在同一侧上两点,$\widehat{DC}$=$\widehat{CB}$,对角线AC交BD于点E,AE=2EC=2.
如图,D、C是以AB为直径的⊙O上被AB分在同一侧上两点,$\widehat{DC}$=$\widehat{CB}$,对角线AC交BD于点E,AE=2EC=2.分析 (1)由已知及相似三角形的性质,圆周角定理可知$\widehat{AD}=\widehat{BC}$,从而可证∠DCA=∠CAB,进而得到DC∥AB,即可证明四边形ABCD为梯形.
(2)由已知及(1)可知,△COB为正三角形,∠CAO=30°,可求梯形的高h=ACsin∠CAO,进而由余弦定理DC,AB的值,利用梯形的面积公式即可计算得解.
解答 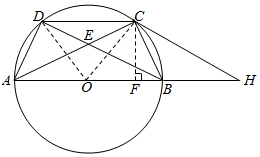 解:(1)证明:过C点作CH∥DB,交AB延长线于H.(如图),连接OC,
解:(1)证明:过C点作CH∥DB,交AB延长线于H.(如图),连接OC,
∵△AEB≈△ACH,
∵BH:AB=EC:AE=1:2
∵BH=$\frac{1}{2}$AB,
∵$\widehat{DC}$=$\widehat{CB}$,
∴C是弧DB中点
∵∠DAB=∠COB (圆周角=$\frac{1}{2}$同弧圆心角),
∠DBA=∠CHO,
∵△ADB≌△OCH,
∵∠OCH=∠ADB=90°,
CH为切线,
∵∠CHA=$\frac{1}{2}$$\widehat{AC}$=∠DBA=$\widehat{AD}$,
∵D为劣弧AC的中点,
∵$\widehat{AD}=\widehat{BC}$,
∵∠DCA=∠CAB,
∵DC∥AB,
∵四边形ABCD为梯形.
(2)∵由已知及(1)可知,△COB为正三角形,∠CAO=30°,
∴梯形的高h=ACsin∠CAO=(2+1)×$\frac{1}{2}$=$\frac{3}{2}$,
∴设⊙O的半径为r,则在△AOC中,由余弦定理可得:9=r2+r2-2r2×(-$\frac{1}{2}$),解得:r=$\sqrt{3}$,
即可得:DC=$\sqrt{3}$,AB=2$\sqrt{3}$,
∴梯形面积S=$\frac{(\sqrt{3}+2\sqrt{3})×\frac{3}{2}}{2}$=$\frac{9\sqrt{3}}{4}$.
点评 本题主要考查了相似三角形的性质,圆周角定理,梯形的面积公式的综合应用,考查了转化思想和数形结合思想的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三棱锥S-ABC中,已知△ABC是以角A为直角的等腰三角形,AB=2,SB=SC=$\sqrt{3}$,SO⊥BC,垂足为O.
三棱锥S-ABC中,已知△ABC是以角A为直角的等腰三角形,AB=2,SB=SC=$\sqrt{3}$,SO⊥BC,垂足为O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
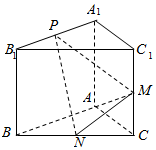 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$(λ∈R).
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$(λ∈R).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com