
分析 作出图象,由题意可得OA=b,OB=a,设OM=x,∠OMA=α,∠OMB=β,由三角函数的定义可得tanα=$\frac{b}{x}$,tanβ=$\frac{a}{x}$,再由两角差的正切公式可得tan(β-α)=$\frac{tanβ-tanα}{1+tanβtanα}$=$\frac{\frac{a}{x}-\frac{b}{x}}{1+\frac{ab}{{x}^{2}}}$=$\frac{a-b}{x+\frac{ab}{x}}$,由基本不等式可得.
解答 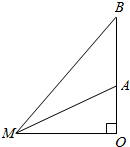 解:如图所示观察者在M处,A、B为画的下、上边缘,
解:如图所示观察者在M处,A、B为画的下、上边缘,
由题意可得OA=b,OB=a,设OM=x,∠OMA=α,∠OMB=β,
则分别在直角三角形中可得tanα=$\frac{b}{x}$,tanβ=$\frac{a}{x}$,
∴tan(β-α)=$\frac{tanβ-tanα}{1+tanβtanα}$
=$\frac{\frac{a}{x}-\frac{b}{x}}{1+\frac{ab}{{x}^{2}}}$=$\frac{a-b}{x+\frac{ab}{x}}$≤$\frac{a-b}{2\sqrt{ab}}$
当且仅当x=$\frac{ab}{x}$即x=$\sqrt{ab}$时取等号,
由∵y=tanx在(0,$\frac{π}{2}$)为增函数,
∴当x=$\sqrt{ab}$时,视角最大.
即观察者离此画$\sqrt{ab}$米时,才能使得视角最大.
故答案为:$\sqrt{ab}$
点评 本题考查基本不等式求最值的实际应用,涉及正切函数的单调性和两角差的正切公式,属中档题.考查学生的转化能力.


科目:高中数学 来源: 题型:选择题
| A. | (-1,$\frac{1}{2}$) | B. | (-1,2) | C. | ($\frac{1}{2}$,2) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | [0,1] | C. | [0,$\sqrt{5}$) | D. | [0,$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
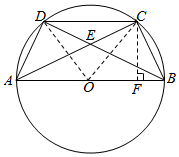 如图,D、C是以AB为直径的⊙O上被AB分在同一侧上两点,$\widehat{DC}$=$\widehat{CB}$,对角线AC交BD于点E,AE=2EC=2.
如图,D、C是以AB为直径的⊙O上被AB分在同一侧上两点,$\widehat{DC}$=$\widehat{CB}$,对角线AC交BD于点E,AE=2EC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{100}{101}$ | B. | $\frac{200}{101}$ | C. | 2 | D. | $\frac{198}{101}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com