
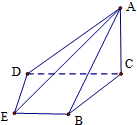
 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.分析 (1)利用梯形的性质求出BC,利用勾股定理得出AC⊥BC,于是AC⊥平面BCDE,得出AC⊥DE,又DE⊥CD得出DE⊥平面BCDE;
(2)VC-ABD=VA-BCD=$\frac{1}{3}$S△BCD•AC.
解答 解:(1)在直角梯形BCDE中,
∵DE=BE=1,CD=2,∴BC=$\sqrt{(2-1)^{2}+{1}^{2}}$=$\sqrt{2}$,
又AB=2,AC=$\sqrt{2}$,
∴AB2=AC2+BC2,即AC⊥BC,
又平面ABC⊥平面BCDE,平面ABC∩平面BCDE=BC,AC?平面ABC,
∴AC⊥平面BCDE,又DE?平面BCDE,
∴AC⊥DE,又DE⊥DC,AC∩CD=C,
∴DE⊥平面ACD.
(2)VC-ABD=VA-BCD=$\frac{1}{3}$S△BCD•AC=$\frac{1}{3}×\frac{1}{2}×2×1×\sqrt{2}$=$\frac{\sqrt{2}}{3}$.
点评 本题考查了线面垂直的判定定理,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$,2 | B. | 2,2 | C. | 3,2 | D. | 2,3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{7}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
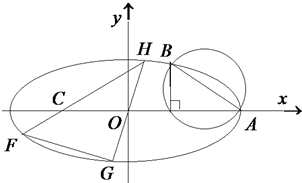 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆E过点$B(2e,\frac{b}{2})$,以AB为直径的圆恰好经过椭圆的右焦点.
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆E过点$B(2e,\frac{b}{2})$,以AB为直径的圆恰好经过椭圆的右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
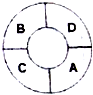 如图,一环形花坛成A,B,C,D四块,现有4种不同的花供选择,要求在每块地里种一种花,且相邻的两块种不同的花,则不同的种法总数为( )
如图,一环形花坛成A,B,C,D四块,现有4种不同的花供选择,要求在每块地里种一种花,且相邻的两块种不同的花,则不同的种法总数为( )| A. | 48 | B. | 60 | C. | 84 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13.1m/s | B. | -13.1m/s | C. | -26.1m/s | D. | 26.1m/s |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\sqrt{41}$ | C. | $\sqrt{15}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com