
| A. | $\sqrt{13}$ | B. | $\sqrt{41}$ | C. | $\sqrt{15}$ | D. | $\sqrt{3}$ |
分析 设|AF1|=t,|AB|=5x,结合|AB|:|BF2|:|AF2|=5:12:13,得到△ABF2为直角三角形,结合勾股定理建立方程关系进行求解即可.
解答 解:设|AF1|=t,|AB|=5x,则|BF2|=12x,|AF2|=13x,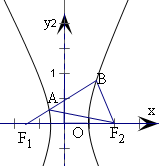
根据双曲线的定义,得|AF2|-|AF1|=|BF1|-|BF2|=2a,
即13x-t=(5x+t)-12x=2a,解得t=10x,x=$\frac{2}{3}$a,
即|AF1|=$\frac{20}{3}$a,|AF2|=$\frac{26}{3}$a,
∵|AB|:|BF2|:|AF2|=5:12:13,∴得△ABF2是以B为直角的Rt△,
则|BF1|=t+5x=10x+5x=15x=15×$\frac{2}{3}$a=10a,
|BF2|=12x=12×$\frac{2}{3}$a=8a,
则|F1F2|2=|BF1|2+|BF2|2,
即100a2+64a2=4c2,
即164a2=4c2,
则41a2=c2,
即c=$\sqrt{41}$a,
因此,该双曲线的离心率e=$\frac{c}{a}$=$\sqrt{41}$.
故选:B.
点评 本题着重考查了双曲线的定义与简单几何性质、直角三角形的判定与性质、利用余弦定理解三角形等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
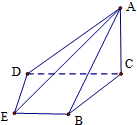 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或5 | B. | 1或3 | C. | 4或6 | D. | 0或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某组合体如图所示,上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.正四棱锥P-EFGH的高为$\sqrt{3}$,EF长为2,AE长为1,则该组合体的表面积为( )
某组合体如图所示,上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.正四棱锥P-EFGH的高为$\sqrt{3}$,EF长为2,AE长为1,则该组合体的表面积为( )| A. | 20 | B. | 4$\sqrt{3}$+12 | C. | 16 | D. | 4$\sqrt{3}$+8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3]∪[1,+∞) | C. | [1,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com