
分析 (Ⅰ)由对数函数y=lgx图象经过点F求出F的纵坐标,得到p,则抛物线方程可求;
(Ⅱ)由题意可知,直线AB的斜率存在,设AB所在直线方程为y=k(x-1),联立直线方程和抛物线方程,由抛物线弦长公式求得|AB|,求出B的横坐标,再由焦半径公式求得|BF|,作商后可知$\frac{|AB|}{|BF|}$不是定值.
解答 解:(Ⅰ)由对数函数y=lgx图象经过点F,可得F(1,0),
∴$\frac{p}{2}=1$,即p=2,则抛物线C的方程为y2=4x;
(Ⅱ)如图,
由题意可知,直线AB的斜率存在,设AB所在直线方程为y=k(x-1),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,得k2x2-(2k2+4)x+k2=0.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=\frac{2{k}^{2}+4}{{k}^{2}}$,x1x2=1.
∴|AB|=${x}_{1}+{x}_{2}+p=\frac{2{k}^{2}+4}{{k}^{2}}+2=\frac{4{k}^{2}+4}{{k}^{2}}$,
由x1x2=1,得${x}_{1}=\frac{1}{{x}_{2}}$,∴$\frac{1}{{x}_{2}}+{x}_{2}+2=\frac{4{k}^{2}+4}{{k}^{2}}=4+\frac{4}{{k}^{2}}$,
解得:${x}_{2}=1+\frac{2}{{k}^{2}}±\frac{2}{{k}^{2}}\sqrt{{k}^{2}+1}$.
∴|BF|=${x}_{2}+\frac{p}{2}=1+\frac{2}{{k}^{2}}±\frac{2}{{k}^{2}}\sqrt{{k}^{2}+1}+1$=$2(1+\frac{1}{{k}^{2}}±\frac{\sqrt{{k}^{2}+1}}{{k}^{2}})$.
则$\frac{|AB|}{|BF|}$=$\frac{\frac{4{k}^{2}+4}{{k}^{2}}}{2\frac{{k}^{2}+1±\sqrt{{k}^{2}+1}}{{k}^{2}}}$=$\frac{2({k}^{2}+1)}{({k}^{2}+1)±\sqrt{{k}^{2}+1}}$,不是定值.
点评 本题主要考查直线与抛物线的位置关系,抛物线的简单性质,特别是焦点弦问题,解题时要善于运用抛物线的定义解决问题,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
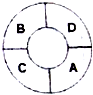 如图,一环形花坛成A,B,C,D四块,现有4种不同的花供选择,要求在每块地里种一种花,且相邻的两块种不同的花,则不同的种法总数为( )
如图,一环形花坛成A,B,C,D四块,现有4种不同的花供选择,要求在每块地里种一种花,且相邻的两块种不同的花,则不同的种法总数为( )| A. | 48 | B. | 60 | C. | 84 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
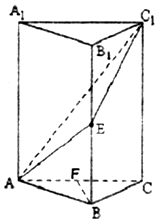 正三棱柱ABC-A1B1C1中,E为BB1的中点,F为AC的中点,AA1=2AB.
正三棱柱ABC-A1B1C1中,E为BB1的中点,F为AC的中点,AA1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\sqrt{41}$ | C. | $\sqrt{15}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{1+3\sqrt{5}}}{8}$ | B. | $\frac{{1+5\sqrt{3}}}{8}$ | C. | $\frac{{1-3\sqrt{5}}}{8}$ | D. | $\frac{{1-5\sqrt{3}}}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com