
| A. | $\frac{5}{7}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{7}$ | D. | $\frac{4}{9}$ |
分析 先求出基本事件总数n=${C}_{9}^{5}$,再求出抽出班级的班号的中位数是5包含的基本事件个数m=${C}_{4}^{2}{C}_{4}^{2}$,由此能求出抽出班级的班号的中位数是5的概率.
解答 解:某校高三年级有班号为1~9的9个班,
从这9个班中任抽5个班级参加一项活动,
基本事件总数n=${C}_{9}^{5}$=126,
抽出班级的班号的中位数是5包含的基本事件个数m=${C}_{4}^{2}{C}_{4}^{2}$=36
∴抽出班级的班号的中位数是5的概率p=$\frac{m}{n}$=$\frac{36}{126}$=$\frac{2}{7}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
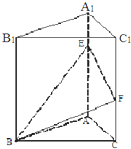 已知三棱柱ABC-A1B1C1中,平面BCC1B1⊥底面ABC,BB1⊥AC,底面ABC是边长为2的等边三角形,AA1=3,E、F分别在棱AA1,CC1上,且AE=C1F=2.
已知三棱柱ABC-A1B1C1中,平面BCC1B1⊥底面ABC,BB1⊥AC,底面ABC是边长为2的等边三角形,AA1=3,E、F分别在棱AA1,CC1上,且AE=C1F=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4) | B. | (4,6) | C. | (2,6) | D. | (6,12) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2016,则i与j的和为( )
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2016,则i与j的和为( )| A. | 80 | B. | 81 | C. | 82 | D. | 83 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
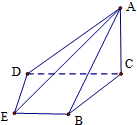 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或5 | B. | 1或3 | C. | 4或6 | D. | 0或2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com