
| A. | (2,4) | B. | (4,6) | C. | (2,6) | D. | (6,12) |
分析 令g(x)=|f(x)|+|f(a-x)|,则g(x)的图象关于x=$\frac{a}{2}$对称,根据对称性可得4×$\frac{a}{2}$=4,从而解出a=2,然后化简g(x)=|f(x)|+|f(2-x)|,再根据图象即可求出t的取值范围
解答 令g(x)=|f(x)|+|f(a-x)|,则g(a-x)=g(x)
故y=g(x)的图象关于x=$\frac{a}{2}$对称
又∵关于x的方程|f(x)|+|f(a-x)|-t=0有四个不同的实根,且所有实根之和为4
∴4×$\frac{a}{2}$=4,得a=2
∴g(x)=|x2-4x|+|(2-x)2-4(2-x)|=|x(x-4)|+|(x-2)(x+2)|
=$\left\{\begin{array}{l}{2{x}^{2}-4x-4,x≥4}\\{4x-4,2<x<4}\\{-2{x}^{2}+4x+4,0<x≤2}\\{-4x+4,-2<x≤0}\\{2{x}^{2}-4x-4,x≤-2}\end{array}\right.$=$\left\{\begin{array}{l}{2(x-1)^{2}-6,x≥4}\\{4x-4,2<x<4}\\{-2(x-1)^{2}+6,0<x≤2}\\{-4x+4,-2<x≤0}\\{2(x-1)^{2}-6,x≤-2}\end{array}\right.$
作出y=g(x)的图象如下
关于x的方程|f(x)|+|f(a-x)|-t=0有四个不同的实根可转化为y=g(x)与y=t的图象有四个不同的交点
故结合图象可得:4<t<6,即t的取值范围为(4,6)
故选B
点评 本题考查了函数的性质应用以及含有绝对值的分段函数的应用,同时还考查了数形结合的数学思想方法,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$,2 | B. | 2,2 | C. | 3,2 | D. | 2,3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
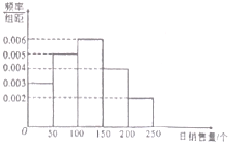 一家面包根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
一家面包根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{7}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
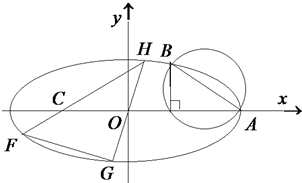 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆E过点$B(2e,\frac{b}{2})$,以AB为直径的圆恰好经过椭圆的右焦点.
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆E过点$B(2e,\frac{b}{2})$,以AB为直径的圆恰好经过椭圆的右焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com