
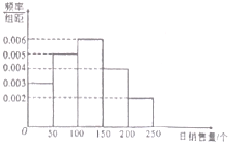
 一家面包根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
一家面包根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.分析 (1)利用频率分布直方图的性质与平均值,中位数的关系即可得出.
(2)销售量不低于100个的概率P=1-(0.003+0.005)×50=0.6,X可能取的值为0,1,2,3,则X~B(3,0.6),利用二项分布列的概率计算公式及其期望方差的计算公式即可得出.
解答 解:(1)①估计平均值为25×0.15+75×0.25+125×0.3+175×0.2+225×0.1=117.5.
②[0,100)的频率为:(0.003+0.005)×50=0.4,[100,150)的频率为0.006×50=0.3,
∴日销售量中位数的估计值为:100+$\frac{0.5-0.4}{0.3}$≈117.
(2)销售量不低于100个的概率P=1-(0.003+0.005)×50=0.6,
X可能取的值为0,1,2,3,则X~B(3,0.6),
相应的概率为P(X=k)=${∁}_{3}^{k}$0.6k•0.43-k(k=0,1,2,3).
随机变量X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 0.064 | 0.288 | 0.432 | 0.216 |
点评 本题考查了频率分布直方图的性质与平均值,中位数的关系、二项分布列的概率计算公式及其期望方差的计算公式,考查了推理能力与计算能力,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
 如图四边形ABCD为正方形,BG,DE,AF两两平行且BG=DE=$\frac{1}{2}$AF=$\frac{1}{2}$AB,又AF垂直底面ABCD.
如图四边形ABCD为正方形,BG,DE,AF两两平行且BG=DE=$\frac{1}{2}$AF=$\frac{1}{2}$AB,又AF垂直底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4) | B. | (4,6) | C. | (2,6) | D. | (6,12) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2016,则i与j的和为( )
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2016,则i与j的和为( )| A. | 80 | B. | 81 | C. | 82 | D. | 83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com