
 如图四边形ABCD为正方形,BG,DE,AF两两平行且BG=DE=$\frac{1}{2}$AF=$\frac{1}{2}$AB,又AF垂直底面ABCD.
如图四边形ABCD为正方形,BG,DE,AF两两平行且BG=DE=$\frac{1}{2}$AF=$\frac{1}{2}$AB,又AF垂直底面ABCD.分析 (1)欲证明CG∥平面ADEF,只需推知平面BCG∥平面ADEF即可.
(2)如图,通过作辅助线构建正方体,结合正方体的性质进行证明即可.
解答 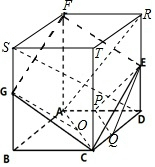 证明:(1)∵BG∥AF,BG?平面ADEF,AF?平面ADEF,
证明:(1)∵BG∥AF,BG?平面ADEF,AF?平面ADEF,
∴BG∥平面ADEF;
同理,BC∥平面ADEF.
又∵BG∩BC=B,
∴平面BCG∥平面ADEF,
∴CG∥平面ADEF;
(2)如图,连接FG,GO,EQ,AC,AR,SD.
∵GO∥SD,平面EPQ∥平面RAC,在正方体中FSTR-ABCD中,显然体对角SD线∥平面RAC,
∴GO⊥平面EPQ.
点评 本题考查直线与平面垂直、平面与平面平行的判定,解题时,注意题中辅助线的作法,这是本题的难点.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
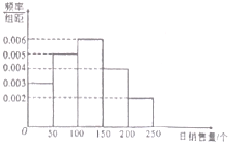 一家面包根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
一家面包根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-2i | B. | 2+i | C. | -$\sqrt{5}$+$\sqrt{5}i$ | D. | $\sqrt{5}$+$\sqrt{5}$i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com