练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．以$2i-\sqrt{5}$的虚部为实部，以$\sqrt{5}i+2{i^2}$的实部为虚部的新复数是（　　）
    A．2-2iB．2+iC．-$\sqrt{5}$+$\sqrt{5}i$D．$\sqrt{5}$+$\sqrt{5}$i

    分析 利用实部与虚部的定义即可得出．

    解答 解：$2i-\sqrt{5}$的虚部为2，以$\sqrt{5}i+2{i^2}$=-2+$\sqrt{5}$i的实部为-2，
    ∴要求的新复数是2-2i，
    故选：A．

    点评 本题考查了实部与虚部的定义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．已知函数f（x）在实数集R上具有下列性质：
    ①f（x+2）=-f（x）；
    ②f（x+1）是偶函数；
    ③当x1≠x2∈[1，3]时，（f（x2）-f（x1））•（x2-x1）＞0，
    则f（2015），f（2016），f（2017）的大小关系为（　　）
    A．f（2015）＞f（2016）＞f（2017）B．f（2016）＞f（2015）＞f（2017）
    C．f（2017）＞f（2015）＞f（2016）D．f（2017）＞f（2016）＞f（2015）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图四边形ABCD为正方形，BG，DE，AF两两平行且BG=DE=$\frac{1}{2}$AF=$\frac{1}{2}$AB，又AF垂直底面ABCD．
     （1）求证：CG∥平面ADEF；
    （2）记正方形ABCD的中心为O，AD，CD的中点分别为P，Q，求证：GO⊥平面EPQ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在△ABC中，若a2+b2＜c2，且sinC=$\frac{1}{2}$，则∠C=（　　）
    A．120°B．60°C．150°D．30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．把正整数按一定的规则排成了如图所示的三角形数表．设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a42=8．若aij=2016，则i与j的和为（　　）
    A．80B．81C．82D．83

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．把y=sin2x的图象按向量$\overrightarrow a$经过一次平移后得到$y=sin（2x+\frac{π}{3}）+2$的图象，则$\overrightarrow a$为（　　）
    A．$（\frac{π}{6}\;，2）$B．$（-\frac{π}{6}\;，2）$C．$（-\frac{π}{6}\;，-2）$D．$（\frac{π}{6}\;，-2）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若方程$\frac{{x}^{2}}{1-k}$+$\frac{{y}^{2}}{2+k}$=1表示椭圆，则k的取值范围为$（-2，-\frac{1}{2}）$∪$（-\frac{1}{2}，1）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

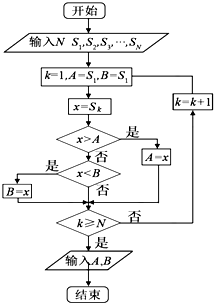    16．设$\overrightarrow{a}$为单位向量，|$\overrightarrow{b}$|=2，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{π}{3}$，两组向量$\overrightarrow{{x}_{1}}$，$\overrightarrow{{x}_{2}}$，$\overrightarrow{{x}_{3}}$，$\overrightarrow{{x}_{4}}$和$\overrightarrow{{y}_{1}}$，$\overrightarrow{{y}_{2}}$，$\overrightarrow{{y}_{3}}$，$\overrightarrow{{y}_{4}}$均由2个$\overrightarrow{a}$和2个$\overrightarrow{b}$排列而成，设S=$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$+$\overrightarrow{{x}_{4}}$•$\overrightarrow{{y}_{4}}$，则把所有的可能结果输入如图框图，则输出的结果为（　　）
    A．A=10，B=4B．A=4，B=10C．A=7，B=4D．A=10，B=7

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知角α的终边经过点（-1，$\sqrt{3}$），则对函数f（x）=sinαcos2x+cosαcos（2x-$\frac{π}{2}$）的表述正确的是（　　）
    A．f（x）在区间$（-\frac{π}{3}，\frac{π}{6}）$上递增
    B．方程f（x）=0在[-$\frac{5}{6}π，0}$]上有三个零点
    C．其中一个对称中心为$（\frac{11}{12}π，0）$
    D．函数y=sin2x向左平移$\frac{π}{3}$个单位可得到f（x）

    查看答案和解析>>

    同步练习册答案