
 设$\overrightarrow{a}$为单位向量,|$\overrightarrow{b}$|=2,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,两组向量$\overrightarrow{{x}_{1}}$,$\overrightarrow{{x}_{2}}$,$\overrightarrow{{x}_{3}}$,$\overrightarrow{{x}_{4}}$和$\overrightarrow{{y}_{1}}$,$\overrightarrow{{y}_{2}}$,$\overrightarrow{{y}_{3}}$,$\overrightarrow{{y}_{4}}$均由2个$\overrightarrow{a}$和2个$\overrightarrow{b}$排列而成,设S=$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$+$\overrightarrow{{x}_{4}}$•$\overrightarrow{{y}_{4}}$,则把所有的可能结果输入如图框图,则输出的结果为( )
设$\overrightarrow{a}$为单位向量,|$\overrightarrow{b}$|=2,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,两组向量$\overrightarrow{{x}_{1}}$,$\overrightarrow{{x}_{2}}$,$\overrightarrow{{x}_{3}}$,$\overrightarrow{{x}_{4}}$和$\overrightarrow{{y}_{1}}$,$\overrightarrow{{y}_{2}}$,$\overrightarrow{{y}_{3}}$,$\overrightarrow{{y}_{4}}$均由2个$\overrightarrow{a}$和2个$\overrightarrow{b}$排列而成,设S=$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$+$\overrightarrow{{x}_{4}}$•$\overrightarrow{{y}_{4}}$,则把所有的可能结果输入如图框图,则输出的结果为( )| A. | A=10,B=4 | B. | A=4,B=10 | C. | A=7,B=4 | D. | A=10,B=7 |
分析 S=$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$+$\overrightarrow{{x}_{4}}$•$\overrightarrow{{y}_{4}}$,$|\overrightarrow{a}|$=1,|$\overrightarrow{b}$|=2,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,$\overrightarrow{a}•\overrightarrow{b}$=1.可得S可能的取值有3种情况,即可得出.
解答 解:S=$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$+$\overrightarrow{{x}_{4}}$•$\overrightarrow{{y}_{4}}$,$|\overrightarrow{a}|$=1,|$\overrightarrow{b}$|=2,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,$\overrightarrow{a}•\overrightarrow{b}$=1.
则S可能的取值有3种情况:S1=$2({\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2})$=10,S2=${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$=7,S3=$4\overrightarrow{a}•\overrightarrow{b}$=4,
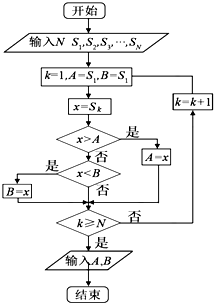
又因为随着k的取值不同,x可以取遍实数S1,S2,SN,依次与A,B比较,
A始终取较大的那个数,B始终取较小的那个数,直到比较完为止,
故最终输出的A,B分别是这N个数中的最大数与最小数,∴A=10,B=4.
故选:A.
点评 本题考查了向量数量积运算性质、分类讨论方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-2i | B. | 2+i | C. | -$\sqrt{5}$+$\sqrt{5}i$ | D. | $\sqrt{5}$+$\sqrt{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1005 | B. | 1006 | C. | 1007 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{3}$ | B. | $-\frac{π}{4}$ | C. | $-\frac{π}{6}$ | D. | $-\frac{π}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com