
分析 (1)对其进行求导,再令导数等于0,即可求出a的值,
(2)g(x)=f(x)+kx(k∈R)在区间(-3,2]上是增函数,可以对其进行求导,将问题转化为g′(x)>0在区间(-3,2]上恒成立,从而求解
解答 解:(1)∵f(x)=ln(x+3)+ax+2,
∴f′(x)=$\frac{1}{x+3}$+a,
∵f(x)在x=-2处取得极值,
∴f′(-2)=$\frac{1}{-2+3}$+a=0,
解得:a=-1,经检验符合题意,
(2)由(1)可知f(x)=ln(x+3)-x+2,
∴g(x)=ln(x+3)+(k-1)x+2,
∴g′(x)=$\frac{1}{x+3}$+k-1
∵g(x)在区间(-3,2]上为增函数,
∴g′(x)>0在区间(-3,2]上恒成立,
即k≥1-$\frac{1}{x+3}$在(-3,2]上恒成立,而1-$\frac{1}{x+3}$在此区间上的最大值为$\frac{4}{5}$,
故k≥$\frac{4}{5}$.
点评 本题主要考查函数的极值与导数的关系,以及利用导数求函数的单调性,综合性比较强;


科目:高中数学 来源: 题型:解答题
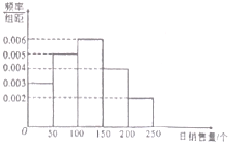 一家面包根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
一家面包根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
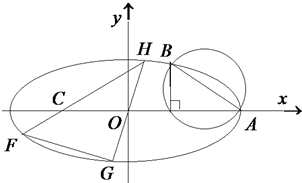 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆E过点$B(2e,\frac{b}{2})$,以AB为直径的圆恰好经过椭圆的右焦点.
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点为A,离心率为e,且椭圆E过点$B(2e,\frac{b}{2})$,以AB为直径的圆恰好经过椭圆的右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13.1m/s | B. | -13.1m/s | C. | -26.1m/s | D. | 26.1m/s |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a-b}$+$\frac{1}{b-c}$>$\frac{4}{a-c}$ | B. | $\frac{1}{a-b}$+$\frac{1}{b-c}$<$\frac{4}{a-c}$ | C. | $\frac{1}{a-b}$+$\frac{1}{b-c}$≥$\frac{4}{a-c}$ | D. | $\frac{1}{a-b}$+$\frac{1}{b-c}$≤$\frac{4}{a-c}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com