
【题目】已知两定点![]() 和
和![]() ,若对于实数
,若对于实数![]() ,函数
,函数![]() (
(![]() )的图像上有且仅有6个不同的点
)的图像上有且仅有6个不同的点![]() ,使得
,使得![]() 成立,则
成立,则![]() 的取值范围是________
的取值范围是________
【答案】![]()
【解析】
画出函数y=|x+2|+|x﹣2|﹣4在[﹣4,4]的图象,讨论若P在AB上,设P(x,﹣2x﹣4);若P在BC上,设P(x,0);若P在CD上,设P(x,2x﹣4).求得向量PE,PF的坐标,求得数量积,由二次函数的最值的求法,求得取值范围,讨论交点个数,即可得到所求范围.
解:函数y=|x+2|+|x﹣2|﹣4
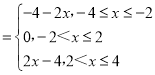 ,
,
(1)若P在AB上,设P(x,﹣2x﹣4),﹣4≤x≤﹣2.
∴![]() (3﹣x,6+2x),
(3﹣x,6+2x),![]() (﹣3﹣x,6+2x).
(﹣3﹣x,6+2x).
∴![]() x2﹣9+(6+2x)2=5x2+24x+27,
x2﹣9+(6+2x)2=5x2+24x+27,
∵x∈[﹣4,﹣2],∴由二次函数的性质可得:当![]() 时有两解;
时有两解;
(2)若P在BC上,设P(x,0),﹣2<x≤2.
∴![]() (3﹣x,2),
(3﹣x,2),![]() (﹣3﹣x,2).
(﹣3﹣x,2).
∴![]() x2﹣9+4=x2﹣5,
x2﹣9+4=x2﹣5,
∵﹣2<x≤2,∴﹣5≤λ≤﹣1.
∴当λ=﹣5或﹣1时有一解,当﹣5<λ<﹣1时有两解;
(3)若P在CD上,设P(x,2x﹣4),2<x≤4.
![]() (3﹣x,6﹣2x),
(3﹣x,6﹣2x),![]() (﹣3﹣x,6﹣2x),
(﹣3﹣x,6﹣2x),
∴![]() x2﹣9+(6﹣2x)2=5x2﹣24x+27,
x2﹣9+(6﹣2x)2=5x2﹣24x+27,
∵2<x≤4,
∴∴由二次函数的性质可得:当![]() 时有两解;
时有两解;
综上,可得有且只有6个不同的点P的情况是![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式:  ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】未来创造业对零件的精度要求越来越高.![]() 打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有发展空间.某制造企业向
打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有发展空间.某制造企业向![]() 高校
高校![]() 打印实验团队租用一台
打印实验团队租用一台![]() 打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取
打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取![]() 个零件,度量其内径的茎叶图如图(单位:
个零件,度量其内径的茎叶图如图(单位:![]() ).
).

(1)计算平均值![]() 与标准差
与标准差![]() ;
;
(2)假设这台![]() 打印设备打印出品的零件内径
打印设备打印出品的零件内径![]() 服从正态分布
服从正态分布![]() ,该团队到工厂安装调试后,试打了
,该团队到工厂安装调试后,试打了![]() 个零件,度量其内径分别为(单位:
个零件,度量其内径分别为(单位:![]() ):
):![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试问此打印设备是否需要进一步调试?为什么?
,试问此打印设备是否需要进一步调试?为什么?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,己知椭圆C:![]() 的左、右顶点为A,B,右焦点为F.过点A且斜率为k(
的左、右顶点为A,B,右焦点为F.过点A且斜率为k(![]() )的直线交椭圆C于另一点P.
)的直线交椭圆C于另一点P.
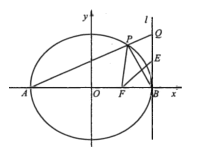
(1)求椭圆C的离心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设直线l:![]() ,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区不同身高![]() 的未成年男孩的体重平均值
的未成年男孩的体重平均值![]() 如下表:
如下表:
身高 | 60 | 70 | 80 | 90 | 100 |
体重 | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(1)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]() ,
,![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com