
分析 (1)根据题意,通过反证法假设结论不成立,通过得出与已知a+b+c=1矛盾,可得结论;
(2)寻找使不等式成立的充分条件,要是不等式成立,只要证 6+7+2$\sqrt{42}$>8+5+4$\sqrt{10}$,即证$\sqrt{42}$>2$\sqrt{10}$,
即证 42>40.
解答 证明:(1)假设a、b、c都大于$\frac{1}{3}$,则a+b+c>1,这与已知a+b+c=1矛盾.
故a、b、c中至少有一个不大于$\frac{1}{3}$…(6分)
(2)要证$\sqrt{6}$+$\sqrt{7}$>2$\sqrt{2}$+$\sqrt{5}$,
只要证 6+7+2$\sqrt{42}$>8+5+4$\sqrt{10}$,
只要证$\sqrt{42}$>2$\sqrt{10}$,
即证42>40.
而42>40 显然成立,
故原不等式成立…(12分)
点评 本题考查反证法的应用,涉及分析法证明不等式,关键是寻找使不等式成立的充分条件,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,BE=$\frac{1}{3}$BC1.
如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,BE=$\frac{1}{3}$BC1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
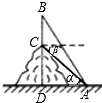 如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高BC为50m,则山高CD等于25$({\sqrt{3}+1})$m.
如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高BC为50m,则山高CD等于25$({\sqrt{3}+1})$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{13}$ | B. | $\frac{2}{13}$ | C. | $\frac{3}{13}$ | D. | $\frac{4}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com