
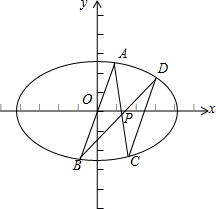
 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{2}}{2}$����A��$\frac{1}{3}$��$\frac{2}{3}$������ԲE�ϣ�����AO����ԲE����һ����ΪB����P��-4t��t������ԲE�ڲ�������AP��BP����ԲE����һ����ֱ�ΪC��D��
��ͼ����ƽ��ֱ������ϵxOy�У���֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{2}}{2}$����A��$\frac{1}{3}$��$\frac{2}{3}$������ԲE�ϣ�����AO����ԲE����һ����ΪB����P��-4t��t������ԲE�ڲ�������AP��BP����ԲE����һ����ֱ�ΪC��D������ ��1������A������Բ���̣�e=$\frac{c}{a}=\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}=\frac{\sqrt{2}}{2}$���������a��b��ֵ�������Բ���̣�
��2�����ݶԳ������B�����꣬$\overrightarrow{AP}$=${��}_{1}\overrightarrow{PC}$��$\overrightarrow{BP}={��}_{2}\overrightarrow{PD}$�����x1��y1��������Բ���̣����$��{��}_{1}+1��•18{t}^{2}={��}_{1}-1$��ͬ����ã���2+1��•18t2=��2-1����ʽ�����æ�1=��2����˿�֤��CD��AB����һ�����ֱ��AB��б�ʣ�����ۿ�֤��
��� ��1���⣺����A������Բ���̵ã�$\frac{��\frac{1}{3}��^{2}}{{a}^{2}}+\frac{��\frac{2}{3}��^{2}}{{b}^{2}}=1$����e=$\frac{c}{a}=\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}=\frac{\sqrt{2}}{2}$��
��ã�a2=1��${b}^{2}=\frac{1}{2}$��
����ԲE�ķ���Ϊ��x2+2y2=1��
��2��֤������A��$\frac{1}{3}$��$\frac{2}{3}$������B��-$\frac{1}{3}$��-$\frac{2}{3}$����
��C��x1��y1����D��x2��y2����$\overrightarrow{AP}$=${��}_{1}\overrightarrow{PC}$��$\overrightarrow{BP}={��}_{2}\overrightarrow{PD}$�����У���1����2�ʣ�0��1����
��$\left\{\begin{array}{l}{{x}_{1}=\frac{��{��}_{1}+1����-4t��-\frac{1}{3}}{{��}_{1}}}\\{{y}_{1}=\frac{��{��}_{1}+1��t-\frac{2}{3}}{{��}_{1}}}\end{array}\right.$��������Բ���̲������ã�$��{��}_{1}+1��•18{t}^{2}={��}_{1}-1$��
ͬ���ã�����2+1��•18t2=��2-1��
��ʽ����ã�����1-��2��•��18t2-1��=0��
�ߵ�P��-4t��t������ԲE�ڲ���
��18t2��1��
���1=��2��
��CD��AB��
��${k}_{AB}=\frac{-\frac{2}{3}-\frac{2}{3}}{-\frac{1}{3}-\frac{1}{3}}=2$��
��ֱ��CD��б��Ϊ��ֵ��
���� ���⿼������Բ�ķ��̣������������߶���֤����ֱ��ƽ�У���ĶԳ��ԣ������ۺϷ������⼰�������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�찲�պϷ�һ�и�����ѧ���¿�һ��ѧ�������Ծ��������棩 ���ͣ������
��֪ ��
�� ����
���� ��
�� �ij�ֶ�����Ҫ��������ʵ��
�ij�ֶ�����Ҫ��������ʵ�� ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�������ѧ�߶����¿�һ��ѧ�������Ծ��������棩 ���ͣ������
ij��˾2016��ǰ�����µ�����λ������Ԫ�����£�
��1�������� �����·�
�����·�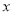 �����Իع鷽�̣�
�����Իع鷽�̣�
��2�����ã�1������õĻع鷽��Ԥ��4�º�5�µ�����
��3�����ã�1������õĻع鷽��Ԥ��ù�˾2016��Ӽ��·ݿ�ʼ����1000��
��ع�ʽ��
 ��
��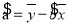 ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�������ѧ�߶����¿�һ��ѧ�������Ծ��������棩 ���ͣ�ѡ����
��������ij����� ���������
���������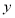 ���ڣ� ��
���ڣ� ��

A��9 B��7 C��13 D��11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
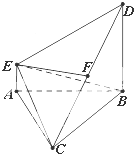 ��ͼ���ڶ�����ABCDE�У�DB��ƽ��ABC��AE��DB���ҡ�ABC�DZ߳�Ϊ2�ĵȱ������Σ�2AE=BD=2��
��ͼ���ڶ�����ABCDE�У�DB��ƽ��ABC��AE��DB���ҡ�ABC�DZ߳�Ϊ2�ĵȱ������Σ�2AE=BD=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $\sqrt{5}$ | C�� | $2\sqrt{2}$ | D�� | $2\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
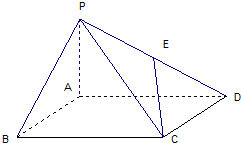
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2+$\sqrt{2}$ | B�� | 2-$\sqrt{2}$ | C�� | 2 | D�� | 2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com