
分析 (1)由题意可知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$(a>b>0)焦点在x轴上,MF2为椭圆通径的一半,即$\frac{1}{2}$×$\frac{2{b}^{2}}{a}$=$\frac{{b}^{2}}{a}$,M点坐标为(c,$\frac{{b}^{2}}{a}$),kMN=${k}_{M{F}_{1}}$=$\frac{\frac{{b}^{2}}{a}-0}{c+c}$=$\frac{3}{4}$,即2b2=3ac,整理得:2c2+3ac-2a2=0,两边同时除以a2,2e2+3e-2=0,解得:e=$\frac{1}{2}$,e=-2,由0<e<1,即可求得C的离心率;
(2)设直线MN与y轴交点为D(0,2),过N作NE⊥y轴,MF2∥y轴,在△MF1F2中,OD为△MF1F2的中位线,求得b2=4a,由|MN|=5|F1N|,丨DF1丨=2丨F1N丨,由△DF1O∽△DNE,根据相似三角形的性质求得N点坐标,代入椭圆方程,由c2=a2-b2,即可求得a和b的值,求得椭圆方程.
解答  解:(1)依题意,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$(a>b>0)焦点在x轴上,MF2为椭圆通径的一半,
解:(1)依题意,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$(a>b>0)焦点在x轴上,MF2为椭圆通径的一半,
即$\frac{1}{2}$×$\frac{2{b}^{2}}{a}$=$\frac{{b}^{2}}{a}$,
∴M点坐标为(c,$\frac{{b}^{2}}{a}$),
由F1(-c,0),依题意有kMN=${k}_{M{F}_{1}}$=$\frac{\frac{{b}^{2}}{a}-0}{c+c}$=$\frac{3}{4}$,即2b2=3ac,…3分
由b2=a2-c2,
∴2c2+3ac-2a2=0,两边同时除以a2,
整理得:2e2+3e-2=0,解得:e=$\frac{1}{2}$,e=-2,
由0<e<1,
∴e=-2(舍),
故椭圆C的离心率为$\frac{1}{2}$;…5分
(2)设直线MN与y轴交点为D(0,2),过N作NE⊥y轴,
依题意,原点O为F1F2的中点,
∴MF2∥y轴,
∴在△MF1F2中,OD为△MF1F2的中位线,
∵D(0,2),
∴$\frac{{b}^{2}}{a}$=4,即b2=4a①…7分
设N(x1,y1),由题意可知:x1<0,y1<0,
由|MN|=5|F1N|,
∴丨DF1丨=2丨F1N丨,
∵△DF1O∽△DNE,
∴$\left\{\begin{array}{l}{\frac{-c}{-{x}_{1}}=\frac{2}{3}}\\{\frac{-{y}_{1}}{2}=\frac{1}{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-\frac{3}{2}c}\\{{y}_{1}=-1}\end{array}\right.$,…9分
代入C的方程,得$\frac{9{c}^{2}}{4{a}^{2}}+\frac{1}{{b}^{2}}=1$②,…10分
由c2=a2-b2③,
将①③代入②中得:$\frac{9({a}^{2}-4a)}{4{a}^{2}}+\frac{1}{4a}=1$,解得:a=7,
b2=4a=28,
∴椭圆的标准方程为:$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{28}=1$.
点评 本题考查椭圆的标准方程及简单几何性质,考查相似三角形的性质,考查数形结合思想,考查计算能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:选择题
已知直线 :
: 与直线
与直线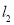 :
: 平行,且
平行,且 与圆
与圆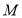 :
: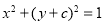 相切,则
相切,则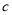 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
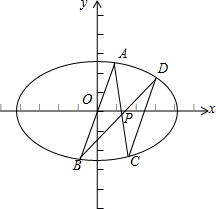 如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点A($\frac{1}{3}$,$\frac{2}{3}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP、BP与椭圆E的另一交点分别为C,D.
如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点A($\frac{1}{3}$,$\frac{2}{3}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP、BP与椭圆E的另一交点分别为C,D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点.
如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 流量(x) | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.
如图,已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为$\frac{π}{3}$的直线t,交l于点A,交圆M于点B,且|AO|=|OB|=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{1+{m^2}}$ | C. | 1 | D. | $\sqrt{1-{m^2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com