
 如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点.
如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点.分析 (1)取AC中点为F,连接BF,证明四边形MEBF是平行四边形,可得ME∥BF,即可证明ME∥平面ABC;
(2)证明ME⊥平面ACD,即可证明平面ADE⊥平面ACD.
解答 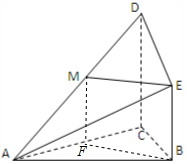 证明:(1)取AC中点为F,连接BF.
证明:(1)取AC中点为F,连接BF.
∵AM=MD,AF=FC,∴MF平行且等于$\frac{1}{2}$DC.
∵BE平行且等于$\frac{1}{2}$DC,∴BE平行且等于MF,
∴四边形MEBF是平行四边形,
∴ME∥BF.
∵ME?平面ABC,BF?平面ABC,
∴ME∥平面ABC;(6分)
(2)∵AF=CF,AB=CB,∴BF⊥AC.
∵DC⊥平面ABC,BF?平面ABC,∴DC⊥BF.
∵DC∩AC=C,∴BF⊥平面ACD.
由(1)中证明可知,ME∥BF.
∴ME⊥平面ACD,
∵ME?平面ADE,
∴平面ADE⊥平面ACD.…(12分)
点评 本题考查空间直线和平面的位置关系,考查空间想象能力、转化、论证能力.


科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:填空题
某服装设计公司有1200名员工,其中老年、中年、青年所占的比例为1:5:6.公司十年庆典活动特别邀请了5位当地的歌手和公司的36名员工同台表演节目,其中员工按老年、中年、青年进行分层抽样,则参演的中年员工的人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
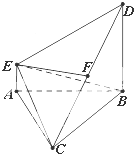 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
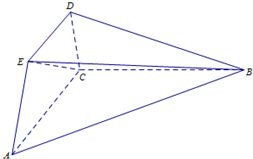 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [1,2] | C. | [-2,0] | D. | [-2,-1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com