
| A. | 2 | B. | $\sqrt{1+{m^2}}$ | C. | 1 | D. | $\sqrt{1-{m^2}}$ |
分析 根据向量的数量积公式和向向量的模的以及二次函数的性质即可求出.
解答 解:∵$|{\overrightarrow a}|=|{\overrightarrow b}$|=1,$\overrightarrow a•\overrightarrow b=m$,
∴|$\overrightarrow{a}$+t$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+2t$\overrightarrow{a}$•$\overrightarrow{b}$+t2|$\overrightarrow{b}$|2=1+2tm+t2=(t+m)2-m2+1,
∴|$\overrightarrow{a}$+t$\overrightarrow{b}$|≥$\sqrt{1-{m}^{2}}$
故选:D.
点评 本题主要考查平面向量的模长公式,两个向量的数量积的定义,二次函数的性质,属中档题.


科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(理)试卷(解析版) 题型:解答题
某公司2016年前三个月的利润(单位:百万元)如下:
(1)求利润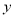 关于月份
关于月份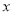 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式:
 ,
,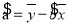 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
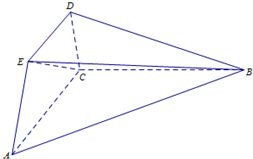 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
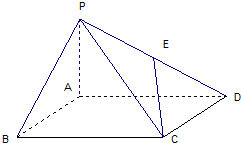
 如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形
如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -2 | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{2}$ | -$\sqrt{2}$ | -1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+$\sqrt{2}$ | B. | 2-$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com