
分析 求出集合M,构造函数y=2x+1-4x-1,通过函数的最值,列出不等式求解即可.
解答 解:不等式x2-x-2≤0的解集为M=[-1,2],令y=2x+1-4x-1=2•2x-$\frac{1}{4}$•(2x)2.
令t=2x,可得y=2t-$\frac{1}{4}{t}^{2}$,t∈[$\frac{1}{2}$,4],函数的对称轴为:t=4,开口向下,t=4即x=2时,y取得最小值,4.对任意x∈M,不等式:2x+1-4x-1≤4-ln($\frac{s-1}{s+1}$)均成立,可得4≤4-ln($\frac{s-1}{s+1}$),
即ln($\frac{s-1}{s+1}$)≤0,解得s>1.
故答案为:s>1.
点评 本题考查函数恒成立以及二次函数的简单性质的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{1+{m^2}}$ | C. | 1 | D. | $\sqrt{1-{m^2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图2所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q,若线段P′B,P′C的中点分别为E,F.
如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图2所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q,若线段P′B,P′C的中点分别为E,F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若θ=90°,则直线PB与平面BCD所成角大小为45° | |
| B. | 若直线PB与平面BCD所成角大小为45°,则θ=90° | |
| C. | 若θ=60°,则直线BD与PC所成角大小为90° | |
| D. | 若直线BD与PC所成角大小为90°,则θ=60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
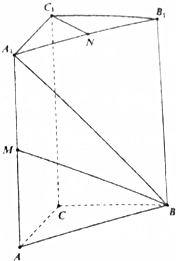 如图所示,在直三棱柱ABC-A1B1C1中,已知CA⊥CB,CA=CB=1,AA1=2,且棱AA1和A1B1的中点分别是M,N.
如图所示,在直三棱柱ABC-A1B1C1中,已知CA⊥CB,CA=CB=1,AA1=2,且棱AA1和A1B1的中点分别是M,N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com