
 如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图2所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q,若线段P′B,P′C的中点分别为E,F.
如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图2所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q,若线段P′B,P′C的中点分别为E,F.分析 (1)假设A、D、E、F四点共面,推导出BC∥AD,与BC∩AD=P矛盾,由此能证明A,D,E,F四点不共面.
(2)几何体P′ADE的体积${V}_{{P}^{'}-ADE}={V}_{E-{P}^{'}AD}$,由此能求出结果.
解答 证明:(1)(反证法)假设A、D、E、F四点共面,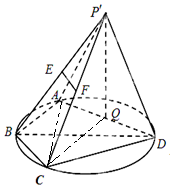
∵EF∥BC,BC?平面AEFD,EF?平面AEFD,
∴BC∥平面AEFD,
又平面AEFD∩平面ABCD=AD,且BC?平面ABCD,
∴BC∥AD,
就与图(1)中BC∩AD=P矛盾,
故假设不成立,即A,D,E,F四点不共面.
解:(2)∵BD是圆的直径,∴∠BAD=∠BCD=$\frac{π}{2}$,
在Rt△ABD和Rt△BCD中,
∵AB=BC=1,BD=2,∴$AD=CD=\sqrt{3}$,且$∠ADB=∠BDC=\frac{π}{6}$,
∴$∠ADC=\frac{π}{3}$,连结AC,则△ACD为正三角形,
又Q为AD中点,连结CQ,则CQ⊥AD,
又点P′在平面ABCD内的射影恰为线段AD的中点Q,
∴P′Q⊥底面ABCD,
AD=AC=DC=$\sqrt{3}$,QC=$\sqrt{3-\frac{3}{4}}$=$\frac{3}{2}$,
设PQ=x,则由切割线定理得:${P}^{'}A({P}^{'}A+\sqrt{3})={P}^{'}B({P}^{'}B+1)$,
即$\sqrt{{x}^{2}+\frac{3}{4}}$($\sqrt{{x}^{2}+\frac{3}{4}}$+$\sqrt{3}$)=$\sqrt{{x}^{2}+\frac{7}{4}}$($\sqrt{{x}^{2}+\frac{7}{4}}+1$),
解得P′Q=x=$\frac{3}{2}$,
∴${S}_{△{P}^{'}AD}=\frac{1}{2}×AD×{P}^{'}Q$=$\frac{1}{2}×\sqrt{3}×\frac{3}{2}$=$\frac{3\sqrt{3}}{4}$,
E到平面P′AD的距离d=$\frac{1}{2}AB$=$\frac{1}{2}$,
∴几何体P′ADE的体积:
${V}_{{P}^{'}-ADE}={V}_{E-{P}^{'}AD}$=$\frac{1}{3}×{S}_{△{P}^{'}AD}×d$=$\frac{1}{3}×\frac{3\sqrt{3}}{4}×\frac{1}{2}$=$\frac{{\sqrt{3}}}{8}$.
点评 本题考查四点不共面的证明,考查几何体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
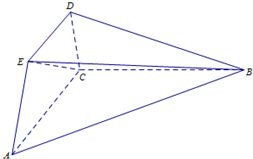 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | [1,2] | C. | [-2,0] | D. | [-2,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com