
分析 (1)由a1=1,${a_{n+1}}=3{a_n}+{2^n}$.变形为${a_{n+1}}+{2^{n+1}}=3({a_n}+{2^n})$,利用等比数列的定义通项公式即可得出.
(2)由(1)知${a_n}={3^n}-{2^n}$,通过放缩3n-2n>2n(n≥2),利用等比数列的求和公式即可得出.
解答 证明:(1)由a1=1,${a_{n+1}}=3{a_n}+{2^n}$.变形为${a_{n+1}}+{2^{n+1}}=3({a_n}+{2^n})$,又a1+2=3,
∴数列$\left\{{{a_n}+{2^n}}\right\}$是以3为首项,3为公比的等比数列.
(2)由(1)知${a_n}={3^n}-{2^n}$,
又3n-2n>2n(n≥2),
∴$\frac{1}{{a}_{n}}$=$\frac{1}{{3}^{n}-{2}^{n}}$$<\frac{1}{{2}^{n}}$
故$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<$1+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n}}$=$\frac{1}{2}+\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=$\frac{3}{2}$-$\frac{1}{{2}^{n}}$<$\frac{3}{2}$.
点评 本题考查了等比数列的定义通项公式、求和公式、放缩法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图2所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q,若线段P′B,P′C的中点分别为E,F.
如图(1)所示,以线段BD为直径的圆经过A,C两点,且AB=BC=1,BD=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点P′位置得到如图2所示的空间图形,其中点P′在平面ABCD内的射影恰为线段AD的中点Q,若线段P′B,P′C的中点分别为E,F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,函数f(x)的图象在P点处的切线方程是y=-2x+17,若点P的横坐标是5,则f(5)+f′(5)=( )
如图,函数f(x)的图象在P点处的切线方程是y=-2x+17,若点P的横坐标是5,则f(5)+f′(5)=( )| A. | 5 | B. | -5 | C. | 10 | D. | -10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
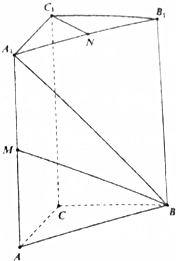 如图所示,在直三棱柱ABC-A1B1C1中,已知CA⊥CB,CA=CB=1,AA1=2,且棱AA1和A1B1的中点分别是M,N.
如图所示,在直三棱柱ABC-A1B1C1中,已知CA⊥CB,CA=CB=1,AA1=2,且棱AA1和A1B1的中点分别是M,N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 栏目1 | 栏目2 | 合计 | |
| 家长 | |||
| 学生 | |||
| 合计 |
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2π | C. | 3π | D. | 4π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com