
【题目】设集合![]()
![]() ,如果存在
,如果存在![]() 的子集
的子集![]() ,
,![]() ,
,![]() 同时满足如下三个条件:
同时满足如下三个条件:
①![]() ;
;
②![]() ,
,![]() ,
,![]() 两两交集为空集;
两两交集为空集;
③![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(Ⅰ) 已知集合![]() ,请判断集合
,请判断集合![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)设集合![]() ,求证:具有性质
,求证:具有性质![]() 的集合
的集合![]() 有无穷多个.
有无穷多个.
【答案】(Ⅰ)不具有,理由见解析;(Ⅱ)证明见解析
【解析】
(Ⅰ)由条件易得集合![]() 具有性质
具有性质![]() ,对集合
,对集合![]() 中的
中的![]() 进行讨论,利用题设条件得出集合
进行讨论,利用题设条件得出集合![]() 不具有性质
不具有性质![]() ;
;
(Ⅱ)利用反证法,假设具有性质![]() 的集合
的集合![]() 有限个,根据题设条件得出矛盾,即可证明具有性质
有限个,根据题设条件得出矛盾,即可证明具有性质![]() 的集合
的集合![]() 有无穷多个.
有无穷多个.
解:(Ⅰ)![]() 具有性质
具有性质![]() ,如可取
,如可取![]() ;
;
![]() 不具有性质
不具有性质![]() ;理由如下:
;理由如下:
对于![]() 中的元素
中的元素![]() ,
,![]() 或者
或者![]()
如果![]() ,那么剩下
,那么剩下![]() 个元素
个元素![]() ,不满足条件;
,不满足条件;
如果![]() ,那么剩下
,那么剩下![]() 个元素
个元素![]() ,也不满足条件.
,也不满足条件.
因此,集合![]() 不具有性质
不具有性质![]() .
.
(Ⅱ)证明:假设符合条件的![]() 只有有限个,设其中元素个数最多的为
只有有限个,设其中元素个数最多的为![]() .
.
对于![]() ,由题设可知,存在
,由题设可知,存在![]() ,
,![]()
![]() 满足条件. 构造如下集合
满足条件. 构造如下集合
![]()
![]()
![]()
由于![]()
所以![]()
易验证![]() ,
,![]() ,
,![]() 对集合
对集合![]() 满足条件,而
满足条件,而![]()
也就是说存在比![]() 的元素个数更多的集合
的元素个数更多的集合![]() 具有性质
具有性质![]() ,与假设矛盾.
,与假设矛盾.
因此具有性质![]() 的集合
的集合![]() 有无穷多个.
有无穷多个.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元,适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
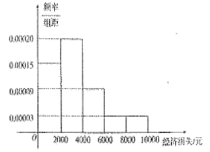
| 经济损失4000元以下 | 经济损失4000元以上 | 合计 |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
(1)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(2)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,李师傅比张师傅早到小区的天数的分布列和数学期望.
附:临界值表
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中有5只同型号的灯泡,其中有3只一等品,2只二等品,现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(Ⅰ)求第一次取到二等品,且第二次取到的是一等品的概率;
(Ⅱ)求至少有一次取到二等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 点
点![]() 为椭圆C上一动点,连接
为椭圆C上一动点,连接![]() ,
,![]() ,设
,设![]() 的角平分线PM交椭圆C的长轴于点
的角平分线PM交椭圆C的长轴于点![]() ,求实数m的取值范围.
,求实数m的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,
,![]() 为圆上任意一点,
为圆上任意一点,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,点
,点![]() ,
,![]() .若点
.若点![]() 为直线
为直线![]() 上一动点,且
上一动点,且![]() 不在
不在![]() 轴上,直线
轴上,直线![]() 、
、![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率等于
轴上,离心率等于![]() ,它的一个顶点恰好在抛物线
,它的一个顶点恰好在抛物线![]() 的准线上.
的准线上.

![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() 点
点![]() ,
,![]() 在椭圆上,
在椭圆上,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点
两侧的动点![]() 当
当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 的焦点是
的焦点是![]() ,
,![]() 是抛物线上的点,H为直线
是抛物线上的点,H为直线![]() 上任一点,A,B分别为椭圆C的上下顶点,且A,B,H三点的连线可以构成三角形.
上任一点,A,B分别为椭圆C的上下顶点,且A,B,H三点的连线可以构成三角形.
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线HA,HB与椭圆C的另一交点分别为点D,E,求证:直线DE过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过点
经过点![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,
,![]() ,
,![]() 点在椭圆上,且满足
点在椭圆上,且满足![]() 的
的![]() 点只有两个.
点只有两个.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的角平分线是
的角平分线是![]() 轴?若存在求出
轴?若存在求出![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 离心率为
离心率为![]() ,
,![]() 、
、![]() 是椭圆C的短轴端点,且
是椭圆C的短轴端点,且![]() 到焦点的距离为
到焦点的距离为![]() ,点M在椭圆C上运动,且点M不与
,点M在椭圆C上运动,且点M不与![]() 、
、![]() 重合,点N满足
重合,点N满足![]() .
.
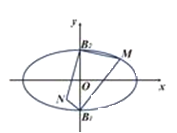
(1)求椭圆C的方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com