Question

16．函数$y={e^x}，y=\frac{e}{x}$与x轴，y轴，x=e所围成的图形的面积为（　　）

• A． 2e-1
• B． 2e+1
• C． 2e+2
• D． 2e-2

Answer 1

分析 先求出$y={e^x}，y=\frac{e}{x}$的交点坐标是（1，e），再由面积与积分的关系将面积用积分表示出来，由公式求出积分，即可得到面积值．

解答 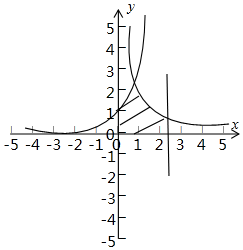解：$y={e^x}，y=\frac{e}{x}$的交点坐标是（1，e），
函数$y={e^x}，y=\frac{e}{x}$与x轴，y轴，x=e所围成的图形的面积为：
S=${∫}_{0}^{1}{e}^{x}dx$+${∫}_{1}^{e}\frac{e}{x}dx$=${e}^{x}{|}_{0}^{1}$+e$lnx{|}_{1}^{e}$=2e-1，
故选：A．

点评 本题考查定积分在求面积中的应用，解答本题关键是根据题设中的条件建立起面积的积分表达式，再根据相关的公式求出积分的值，用定积分求面积是其重要运用，掌握住一些常用函数的导数的求法是解题的知识保证．