练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设曲线在点x处的切线斜率为k(x)，且k(－1)＝0．对一切实数x，不等式x≤k　(x)≤恒成立(a≠0)．

    (1)求k(1)的值；

    (2)求函数k(x)的表达式；

    (3)求证:＞

    答案：
    解析：

    　　(1)由，所以

    　　(2)，由，得

    　　

    　　又恒成立，则由恒成立得

    　　，同理由恒成立也可得

    　　综上，，所以

    　　(3)

    　　要证原不等式式，即证

    　　因为

    　　所以

    　　＝

    　　所以

    　　本小问也可用数学归纳法求证．证明如下：

    　　由

    　　1．当时，左边＝1，右边＝，左边右边，所以，不等式成立

    　　2D．假设当时，不等式成立，即

    　　当时，左边＝

    　　

    　　由

    　　所以

    　　即当时，不等式也成立

    　　综上得


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：荆门市2008届高三第一轮复习导数单元测试卷 题型：044

    设曲线在点x处的切线斜率为k(x)，且k(－1)＝0．对一切实数x，不等式x≤k(x)≤恒成立(a≠0)．

    (1)求f(1)的值；

    (2)求函数k(x)的表达式；

    (3)求证：＞．

    查看答案和解析>>

    科目：高中数学 来源：2012高三数学一轮复习单元练习题　导数(2) 题型：044

    设曲线在点x处的切线斜率为k(x)，

    且k(－1)＝0．对一切实数x，不等式x≤k(x)≤恒成立(a≠0)．

    (1)求f(1)的值；

    (2)求函数k(x)的表达式；

    (3)求证：＞．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

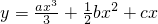    设曲线数学公式在点x处的切线斜率为k（x），且k（-1）=0，对一切实数x，不等式数学公式恒成立（a≠0）．
    （1）求k（1）的值；
    （2）求函数k（x）的表达式．

    查看答案和解析>>

    科目：高中数学 来源：2010年湖北省荆门市龙泉中学高三数学综合训练6（理科）（解析版） 题型：解答题

    设曲线在点x处的切线斜率为k（x），且k（-1）=0，对一切实数x，不等式恒成立（a≠0）．
    （1）求k（1）的值；
    （2）求函数k（x）的表达式．

    查看答案和解析>>

    同步练习册答案