
【题目】如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切).已知环湖弯曲路段为某三次函数图像的一部分,则该函数的解析式为( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1 , y1)∈M,存在(x2 , y2)∈M,使x1x2+y1y2=0成立,则称集合M是“垂直对点集”,给出下列四个集合: ①M={(x,y)|y= ![]() };
};
②M={(x,y)|y=sinx+1};
③={(x,y)|y=2x﹣2};
④M={(x,y)|y=log2x}
其中是“垂直对点集”的序号是( )
A.②③④
B.①②④
C.①③④
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣a(lnx+x).
(1)若函数f(x)恒有两个零点,求a的取值范围;
(2)若对任意x>0,恒有不等式f(x)≥1成立. ①求实数a的值;
②证明:x2ex>(x+2)lnx+2sinx.
查看答案和解析>>
科目:高中数学 来源: 题型:
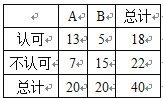
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:
附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣1|﹣|x+2|.
(Ⅰ)解不等式f(x)>0;
(Ⅱ)若x0∈R,使得f(x0)+2m2<4m,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年郴州市两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题时百姓最为关心的热点,参与调查者中关注此问题的约占80%,现从参与者中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示. 
(1)求出频率分布直方图中的a值,并求出这200的平均年龄;
(2)现在要从年龄较小的第1,2,3组用分层抽样的方法抽取12人,再从这12人中随机抽取3人赠送礼品,求抽取的3人中至少有1人的年龄在第3组的概率;
(3)若要从所有参与调查的人(人数很多)中随机选出3人,记关注民生问题的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C的参数方程为 ![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为  (t为参数)以坐标原点O为极点,x轴的正半轴为极轴的极坐标系.
(t为参数)以坐标原点O为极点,x轴的正半轴为极轴的极坐标系.
(1)写出直线l的普通方程以及曲线C的极坐标方程;
(2)若直线l与曲线C的两个交点分别为M,N,直线l与x轴的交点为P,求|PM||PN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分别为PB,BC的中点.
(1)求证:DE∥平面PAC;
(2)求证:DE⊥AD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)满足f(x)=x2﹣2x﹣3(x>0).
(Ⅰ) 若函数g(x)=|f(x)|﹣a有4个零点,求实数a的取值范围;
(Ⅱ) 求|f(x+1)|≤4的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com