
【题目】如图所示,在等腰直角三角形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,现沿
,现沿![]() 将
将![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
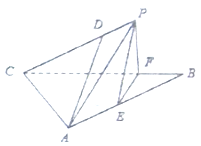
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)设曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,若
,若![]() 与点
与点![]() 的距离为
的距离为![]() ,求
,求![]() 的值;
的值;
(2)若对于任意实数![]() ,
, ![]() 恒成立,试确定
恒成立,试确定![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一个巨大的汽油灌,已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击相互独立,且命中概率都是![]() ,求(1)油罐被引爆的概率;(2)如果引爆或子弹打光则停止射击,设射击次数为
,求(1)油罐被引爆的概率;(2)如果引爆或子弹打光则停止射击,设射击次数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校计划面向高一年级1240名学生开设校本选修课程,为确保工作的顺利实施,按性别进行分层抽样,现抽取124名学生对社会科学类、自然科学类这两大类校本选修课程进行选课意向调查,其中男生有65人.在这124名学生中选修社会科学类的男生有22人、女生有40人.
(1)根据以上数据完成下列列联表;
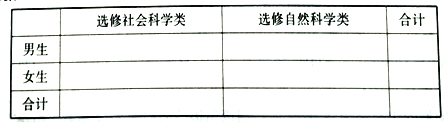
(2)判断能否有99.9%的把握认为科类的选修与性别有关?
附: 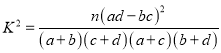 ,其中
,其中![]()
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线
轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为
![]() (
(![]() 为参数,
为参数, ![]() 为直线的倾斜角).
为直线的倾斜角).
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有唯一的公共点,求角
有唯一的公共点,求角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
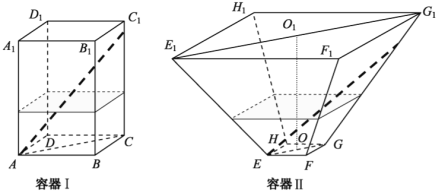
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线
cm,容器Ⅱ的两底面对角线![]() ,
,![]() 的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于点A处,另一端置于侧棱
的一端置于点A处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度;
没入水中部分的长度;
(2)将![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于点E处,另一端置于侧棱
的一端置于点E处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度.
没入水中部分的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com