练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中,以原点为极点, 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位．已知曲线的极坐标方程为,直线的参数方程为

    （为参数, 为直线的倾斜角）．

    （1）写出直线的普通方程和曲线的直角坐标方程；

    （2）若直线与曲线有唯一的公共点,求角的大小．

    【答案】（1）；（2）或

    【解析】试题分析：（I）当时，直线与轴可得直线普通方程为，当时，消去参数即可得到直线的普通方程；在极坐标方程两边同乘以，由极坐标与直角坐标的互化公式即可得到曲线的直角坐标方程；（II）由圆心到直线的距离小于等于半径求之即可.

    试题解析：（I）当时，直线的普通方程为；

    当时，直线的普通方程为.

    ，即为曲线的直角坐标方程.

    （II）当直线的普通方程为，不符合

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】甲、乙两企业生产同一种型号零件，按规定该型号零件的质量指标值落在内为优质品.从两个企业生产的零件中各随机抽出了500件，测量这些零件的质量指标值，得结果如下表：

    甲企业：

    乙企业：

    （1）已知甲企业的500件零件质量指标值的样本方差，该企业生产的零件质量指标值服从正态分布，其中近似为质量指标值的样本平均数（注：求时，同一组数据用该区间的中点值作代表），近似为样本方差，试根据该企业的抽样数据，估计所生产的零件中，质量指标值不低于71.92的产品的概率.（精确到0.001）

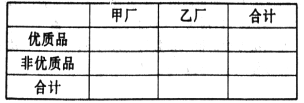
    （2）由以上统计数据完成下面列联表，并问能否在犯错误的概率不超过0.01的前提下，认为“两个分厂生产的零件的质量有差异”.

    附注：

    参考数据： ，

    参考公式： ， ，

    .

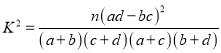
    0.50

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在等腰直角三角形中， ， 为的中点，点在上，且，现沿将折起到的位置，使，点在上，且.

    (1)求证： 平面；

    (2)求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】冬季昼夜温差大小与某反季节大豆新品种发芽多少之间有关系，某农科所对此关系进行了调查分析，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天100颗种子中的发芽数，得到如下资料：

    日期

    12月1日

    12月2日

    12月3日

    12月4日

    12月5日

    温差

    10

    11

    13

    12

    8

    发芽数

    23

    25

    30

    26

    16

    该农科所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验.

    （1）求选取的2组数据恰好是不相邻2天数据的概率；

    （2）若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求出关于的线性回归方程；

    （3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠？

    （参考公式： ， ）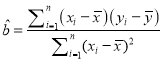

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）已知函数是自然对数的底数， .

    （1）求函数的单调递增区间；

    （2）若为整数， ，且当时， 恒成立，其中为的导函数，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数， ，则对于不同的实数，函数的单调区间个数不可能是（ ）

    A. 1个 B. 2个 C. 3个 D. 5个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， 是的导函数.

    （1）求的极值；

    （2）证明：对任意实数，都有恒成立；

    （3）若在时恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有4个人参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择，为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏．

    （1） 求出4个人中恰有2个人去 参加甲游戏的概率；

    （2）求这4个人中去参加甲游戏人数大于去参加乙游戏的人数的概率；

    （3）用分别表示这4个人中去参加甲、乙游戏的人数，记,求随机变量的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|x2﹣6x+8＜0}，B={x|（x﹣a）（x﹣3a）＜0}．
    （1）若a=1，求A∩B；
    （2）若A∩B=，求a的取值范围．

    查看答案和解析>>

    同步练习册答案