Question

14．在区间[-1，1]上任取两个数a，b，在下列条件时，分别求不等式x²+2ax+b²≥0恒成立时的概率：
（1）当a，b均为整数时；
（2）当a，b均为实数时．

Answer 1

分析 （1）x²+2ax+b²≥0恒成立的充要条件为4a²-4b²≤0，即a²≤b²，用列举法求出基本事件数，然后直接利用古典概型概率计算公式求解；
（2）由题意求出点（a，b）所构成的正方形的面积，再由线性规划知识求出满足a²≤b²的区域面积，由测度比是面积比求概率．

解答 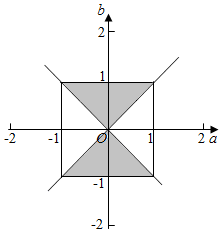解：设事件A为“x²+2ax+b²≥0恒成立”．
x²+2ax+b²≥0恒成立的充要条件为4a²-4b²≤0，即a²≤b²．
（1）基本事件共9个：（-1，-1），（-1，0），（-1，1），（0，-1），（0，0），（0，1），（1，-1），（1，0），（1，1）．其中第一个数表示a的取值，第二个数表示b的取值．
事件A中包含7个基本事件：（-1，-1），（-1，1），（0，-1），（0，0），（0，1），（1，-1），（（1，1）．
事件A发生的概率为P（A）=$\frac{7}{9}$；
（2）试验的全部结果所构成的区域为{（a，b）|-1≤a≤1，-1≤b≤1}．
构成事件A的区域为{（a，b）|-1≤a≤1，-1≤b≤1，a²≤b²}．
如图
∴当a，b均为实数时，不等式x²+2ax+b²≥0恒成立的概率为$\frac{1}{2}$．

点评 本题考查了古典概型及其概率计算公式，考查了几何概型的概率，关键是理解（2）的测度比，是基础题．