
| A. | (0,1) | B. | (0,+∞) | C. | (0,$\frac{1}{3}$)∪($\frac{1}{3}$,1)∪(1,+∞) | D. | ($\frac{1}{3}$,+∞) |
分析 设直线l:y=kx-1,代入抛物线的方程,运用判别式大于0和韦达定理、中点坐标公式可得M的坐标,再由直线的斜率公式可得PM的斜率和方程,令x=0,求得b的解析式,由k的范围,可得b的范围.
解答 解:设直线l:y=kx-1,代入抛物线y2=x,
可得k2x2-(2k+1)x+1=0,(k≠0),
则△=(2k+1)2-4k2=4k+1>0,即k>-$\frac{1}{4}$①
设A(x1,y1),B(x2,y2),
即有x1+x2=$\frac{2k+1}{{k}^{2}}$,
可得M($\frac{2k+1}{2{k}^{2}}$,$\frac{1}{2k}$),
由x1,x2>0,可得x1+x2=$\frac{2k+1}{{k}^{2}}$>0,
即为k>-$\frac{1}{2}$,且k≠0②
由①②可得k>-$\frac{1}{2}$且k≠0,
即有直线PM的方程为y-1=$\frac{\frac{1}{2k}-1}{\frac{2k+1}{2{k}^{2}}-4}$(x-4),
即为y-1=$\frac{k}{1+4k}$(x-4),k≠$\frac{1}{2}$,
令x=0,可得b=1-$\frac{4k}{1+4k}$=$\frac{1}{1+4k}$,
由k>-$\frac{1}{2}$且k≠0,k≠$\frac{1}{2}$,可得:
b>0,且b≠$\frac{1}{3}$,b≠1.
即有b的取值范围是(0,$\frac{1}{3}$)∪($\frac{1}{3}$,1)∪(1,+∞).
故选:C.
点评 本题考查直线和抛物线方程联立,运用判别式大于0,韦达定理和中点坐标公式,以及直线方程和截距的概念,考查运算能力,属于中档题.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
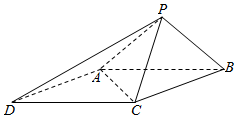 如图,已知四棱锥P-ABCD的底面ABCD为菱形,且∠ABC=60°,
如图,已知四棱锥P-ABCD的底面ABCD为菱形,且∠ABC=60°,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com