
分析 (1)求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间即可;(2)根据函数的单调性,求出函数的极值和端点值,从而求出函数在闭区间上的最值即可.
解答 解:(1)∵f(x)=x3-2x2+x,
∴f′(x)=3x2-4x+1=(3x-1)(x-1),
令f′(x)>0,解得:x>1或x<$\frac{1}{3}$,
令f′(x)<0,解得:$\frac{1}{3}$<x<1,
∴f(x)在(-∞,$\frac{1}{3}$)递增,在($\frac{1}{3}$,1)递减,在(1,+∞)递增;
(2)由(1)得:f(x)在[$\frac{1}{3}$,1)递减,在(1,2]递增;
而f(1)=0,f($\frac{1}{3}$)=$\frac{4}{27}$,f(2)=2,
∴f(x)的最大值为f(2)=2,f(x)的最小值为f(1)=0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道基础题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
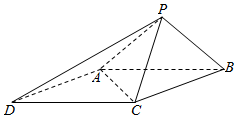 如图,已知四棱锥P-ABCD的底面ABCD为菱形,且∠ABC=60°,
如图,已知四棱锥P-ABCD的底面ABCD为菱形,且∠ABC=60°,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com