
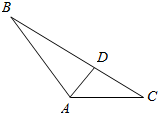
 如图所示.在△ABC中,∠BAC=120°,AB=2,AC=1,D为线段BC上-点.
如图所示.在△ABC中,∠BAC=120°,AB=2,AC=1,D为线段BC上-点.分析 (1)可根据余弦定理求出$BC=\sqrt{7}$,从而得出BD=$\frac{2\sqrt{7}}{3}$,DC=$\frac{\sqrt{7}}{3}$,可设AD=x,从而在△ABD和△ADC中,分别用余弦定理可求出cos∠ADB和cos∠ADC,从而根据cos∠ADB=-cos∠ADC即可求出x,从而求出cos∠ADB,这样根据向量数量积的计算公式即可得出$\overrightarrow{AD}•\overrightarrow{BC}$;
(2)O为三角形的重心时,便可让D为BC边的中点,从而上面的BD=2DC,就变成了BD=DC,这样求$\overrightarrow{AD}•\overrightarrow{BC}$的过程同上面一样了,即把上面的BD,DC的长度换成$\frac{\sqrt{7}}{2}$即可;
(3)当D为线段BC上的动点时,可设BD=kBC,0≤k≤1,从而得出BD=$\sqrt{7}k$,DC=$\sqrt{7}(1-k)$,这样将上面的BD,DC的值换成现在的值,即可用k表示出$\overrightarrow{AD}•\overrightarrow{BC}$,从而由k的范围即可得出$\overrightarrow{AD}•\overrightarrow{BC}$的范围.
解答 解:(1)在△ABC中,由余弦定理得:$B{C}^{2}=4+1-4•(-\frac{1}{2})=7$,∴$BC=\sqrt{7}$;
∵BD=2DC;
∴$BD=\frac{2\sqrt{7}}{3}$,$DC=\frac{\sqrt{7}}{3}$;
设AD=x,则由余弦定理:cos$∠ADB=\frac{{x}^{2}+\frac{28}{9}-4}{2x•\frac{2\sqrt{7}}{3}}$,cos$∠ADC=\frac{{x}^{2}+\frac{7}{9}-1}{2x•\frac{\sqrt{7}}{3}}$;
∴$\frac{{x}^{2}+\frac{28}{9}-4}{2x•\frac{2\sqrt{7}}{3}}=-\frac{{x}^{2}+\frac{7}{9}-1}{2x•\frac{\sqrt{7}}{3}}$;
解得$x=\frac{2}{3}$;
∴$cos∠ADB=\frac{\frac{4}{9}+\frac{28}{9}-4}{\frac{4}{3}•\frac{2\sqrt{7}}{3}}=-\frac{\sqrt{7}}{14}$;
∴$\overrightarrow{AD}•\overrightarrow{BC}=|\overrightarrow{AD}||\overrightarrow{BC}|cos∠ADB$=$\frac{2}{3}×\sqrt{7}×(-\frac{\sqrt{7}}{14})=-\frac{1}{3}$;
(2)设D为BC的中点,则BD=DC=$\frac{\sqrt{7}}{2}$;
同样设AD=x,则:$\frac{{x}^{2}+\frac{7}{4}-4}{2x•\frac{\sqrt{7}}{2}}=-\frac{{x}^{2}+\frac{7}{4}-1}{2x•\frac{\sqrt{7}}{2}}$;
解得$x=\frac{\sqrt{3}}{2}$,∴$AO=\frac{\sqrt{3}}{3}$;
∴$cos∠ADB=\frac{\frac{3}{4}+\frac{7}{4}-4}{\sqrt{3}•\frac{\sqrt{7}}{2}}=-\frac{\sqrt{21}}{7}$;
∴$\overrightarrow{AO}•\overrightarrow{BC}=\frac{\sqrt{3}}{3}×\sqrt{7}×(-\frac{\sqrt{21}}{7})=-1$;
(3)若D为动点,设AD=x,BD=kBC=$\sqrt{7}k$,(0≤k≤1),DC=$\sqrt{7}(1-k)$;
则:$\frac{{x}^{2}+7{k}^{2}-4}{2x•\sqrt{7}k}=-\frac{{x}^{2}+7(1-k)^{2}-1}{2x•\sqrt{7}(1-k)}$;
解得x2=7k2-10k+4,$x=\sqrt{7{k}^{2}-10k+4}$;
∴$cos∠ADB=\frac{7{k}^{2}-10k+4+7{k}^{2}-4}{2\sqrt{7{k}^{2}-10k+4}•\sqrt{7}k}$;
∴$\overrightarrow{AD}•\overrightarrow{BC}=\sqrt{7{k}^{2}-10k+4}•\sqrt{7}$$•\frac{7{k}^{2}-10k+4+7{k}^{2}-4}{2\sqrt{7{k}^{2}-10k+4}•\sqrt{7}k}$=7k-5;
∴①k=0时,D与B重合,由余弦定理得cos∠ABC=$\frac{4+7-1}{4\sqrt{7}}=\frac{5\sqrt{7}}{14}$;
∴$\overrightarrow{AD}•\overrightarrow{BC}=\overrightarrow{AB}•\overrightarrow{BC}•(-cos∠ABC)$=$2\sqrt{7}•(-\frac{5\sqrt{7}}{14})=-5$;
②0<k≤1时,-5<7k-5≤2;
∴$-5≤\overrightarrow{AD}•\overrightarrow{BC}≤2$;
∴$\overrightarrow{AD}•\overrightarrow{BC}$的取值范围为[-5,2].
点评 考查余弦定理,向量数量积的计算公式,这三问中点D的位置不同,而解决问题的方法和过程一样,三角形重心的性质.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow 0$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{BC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-4,4} | B. | {-4,0,4} | C. | {-4,0} | D. | {0} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com