
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 首先理解[x]表示的含义,再结合0<a<1求出[a+$\frac{1}{30}$]+[a+$\frac{2}{30}$]+[a+$\frac{3}{30}$]+…+[a+$\frac{29}{30}$],29个数中有多少个为1,有多少个为0,然后求出a的取值范围,最后再根据[x]的含义求出[10a]的值.
解答 解:∵0<a+$\frac{1}{30}$<a+$\frac{2}{30}$<…<a+$\frac{29}{30}$<2,
∴[a+$\frac{1}{30}$],[a+$\frac{2}{30}$],[a+$\frac{3}{30}$],…,[a+$\frac{29}{30}$],等于0或1
由题设[a+$\frac{1}{30}$]+[a+$\frac{2}{30}$]+[a+$\frac{3}{30}$]+…+[a+$\frac{29}{30}$]=18知,
其中有18个等于1,
所以[a+$\frac{1}{30}$]=[a+$\frac{2}{30}$]=…=[a+$\frac{11}{30}$]=0,
[a+$\frac{12}{30}$]=[a+$\frac{13}{30}$]=…=[a+$\frac{29}{30}$]=1,
所以0<a+$\frac{11}{30}$<1,1≤a+$\frac{12}{30}$<2
故18≤30a<19,于是6≤10a<$\frac{19}{30}$,所以[10a]=6,
故选:6.
点评 本题主要考查取整函数的知识点,解答本题的关键之处是求出[a+$\frac{1}{30}$],[a+$\frac{2}{30}$],…,[a+$\frac{29}{30}$]这29个数中有多少个为1,有多少个为0,否则本题很容易出错,本题难度较大.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:填空题
| ξ | -1 | 0 | 1 |
| P | 0.5 | 1-$\frac{3q}{2}$ | q2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
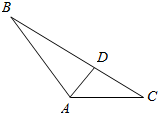 如图所示.在△ABC中,∠BAC=120°,AB=2,AC=1,D为线段BC上-点.
如图所示.在△ABC中,∠BAC=120°,AB=2,AC=1,D为线段BC上-点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com