
 x∈A,试判断g(x)的单调性;(不证)
x∈A,试判断g(x)的单调性;(不证) >2x+a-5},若A∩B≠Φ,求实数a的取值范围.
>2x+a-5},若A∩B≠Φ,求实数a的取值范围.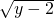 ,x=-1-
,x=-1-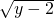
 x∈[2,3]
x∈[2,3] =-1+
=-1+ x∈[2,3]
x∈[2,3] >2x+a-5在集合A上有解,
>2x+a-5在集合A上有解, -2x+5在集合A上有解,
-2x+5在集合A上有解, -2x+5,
-2x+5, -2x+5=
-2x+5= -2x+4 在区间A上单调递减
-2x+4 在区间A上单调递减 ?a<
?a<
 )
) 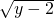 即可得到函数f(x)的反函数;
即可得到函数f(x)的反函数; -2x+5在集合A上有解;再根据函数的单调性求出h(x)=
-2x+5在集合A上有解;再根据函数的单调性求出h(x)= -2x+5在集合A上的最大值,即可得到结论.
-2x+5在集合A上的最大值,即可得到结论.

科目:高中数学 来源: 题型:阅读理解
|
| 10-x |
| 10+x |
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
| 10-x |
| 10+x |
| 10-x |
| 10+x |
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
仔细阅读下面问题的解法:
设A=[0, 1],若不等式21-x-a>0在A上有解,求实数a的取值范围。
解:由已知可得 a < 21-x
令f(x)= 21-x ,∵不等式a <21-x在A上有解,
∴a <f(x)在A上的最大值.
又f(x)在[0,1]上单调递减,f(x)max =f(0)=2. ∴实数a的取值范围为a<2.
研究学习以上问题的解法,请解决下面的问题:
(1)已知函数f(x)=x2+2x+3(-2≤x≤-1),求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=![]() ,x∈A,试判断g(x)的单调性(写明理由,不必证明);
,x∈A,试判断g(x)的单调性(写明理由,不必证明);
(3)若B ={x|![]() >2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。
>2x+a–5},且对于(1)中的A,A∩B≠F,求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源:2014届江西省南昌市高三上学期第一次月考理科数学试卷(解析版) 题型:解答题
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x+a>0在A上有解,求实数a的取值范围.
解:令f(x)=21-x+a,因为f(x)>0在A上有解。

=2+a>0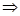 a>-2
a>-2
学习以上问题的解法,解决下面的问题,已知:函数f(x)=x2+2x+3(-2≤x≤-1).
①求f(x)的反函数f-1(x)及反函数的定义域A;
②设B=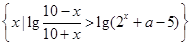 ,若A∩B≠
,若A∩B≠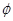 ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
解;令f(x)=21-x+a,∵f(x)>0在A上有解,∴f(x)在A上的最大值大于0.又∵f(x)在[0,1]上单调递减,
∴f(x)max=f(0)=2+a>0,∴a>-2.
学习以上问题的解法,解决下面的问题:已知函数f(x)=x2+2x+3(-2≤x≤-1).
(1)求f(x)的反函数f-1(x)及反函数的定义域A;
(2)设B={x|lg![]() >lg(2x+a-5)},若A∩B≠
>lg(2x+a-5)},若A∩B≠![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com